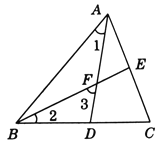
题目内容
【题目】![]() 分别是三角形
分别是三角形![]() 的边
的边![]() 的中点,
的中点,![]() 是
是![]() 所在平面上的动点,连接
所在平面上的动点,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点,顺次连接点
的中点,顺次连接点![]()

(1)如图,当点![]() 在
在![]() 的内部时,求证:四边形
的内部时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 是菱形,则
是菱形,则![]() 与
与![]() 应满足怎样的关系?若四边形
应满足怎样的关系?若四边形![]() 是矩形,则
是矩形,则![]() 与
与![]() 应满足怎样的关系?(直接写出答案,不需要说明理由)
应满足怎样的关系?(直接写出答案,不需要说明理由)
【答案】(1)见解析;(2)OA=OB,![]()
【解析】
(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC且DE=![]() BC,GF∥BC且GF=
BC,GF∥BC且GF=![]() BC,从而得到DE∥GF,DE=GF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
BC,从而得到DE∥GF,DE=GF,再利用一组对边平行且相等的四边形是平行四边形证明即可;
(2)根据邻边相等的平行四边形是菱形,有一个角是直角的平行四边形是矩形解答.
![]() 分别是
分别是![]() 的中点.
的中点.
![]()
![]() 分别是
分别是![]() 的中点
的中点
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() 若四边形
若四边形![]() 是菱形,则DG=GF,
是菱形,则DG=GF,
由(1)中位线可知GF平行且等于![]() BC,DG平行且等于
BC,DG平行且等于![]() AO
AO
∴![]()
若四边形![]() 是矩形,则DG⊥GF,
是矩形,则DG⊥GF,
∵DG∥AO,GF∥BC
∴![]()

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目