Question

【题目】如图，已知正方形中，点在边上，把线段绕点旋转，使点落在直线上的点处，则_________________．

Answer 1

【答案】或

【解析】

根据正方形的性质可得AB＝AD，∠ABC＝∠D＝90°，再根据旋转的性质可得AF＝AE，然后利用“HL”证明Rt△ABF和Rt△ADE全等，根据全等三角形对应边相等可得BF＝DE，再求出正方形的边长为3，然后分点F在线段BC上和CB的延长线上两种情况讨论求解．

解:

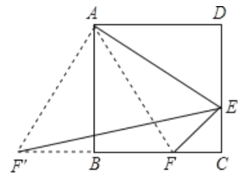
在正方形ABCD中，AB＝AD，∠ABC＝∠D＝90°，

由旋转的性质得，AF＝AE，

在Rt△ABF和Rt△ADE中，

AF＝AE

AB＝AD，

∴Rt△ABF≌Rt△ADE（HL），

∴BF＝DE＝2，

∵DE＝2，EC＝1，

∴正方形的边长为2＋1＝3，

①点F在线段BC上时，FC＝32＝1，

∴EF＝；

②点F在CB的延长线上时，FC＝3＋2＝5，

∴EF′＝，

综上所述，EF的长为

或

故答案为：或．