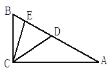题目内容
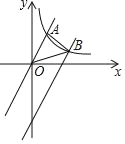
【题目】已知直线 y=kx+b(k≠0)过点 F(0,1),与抛物线 ![]() 相交于B、C 两点
相交于B、C 两点
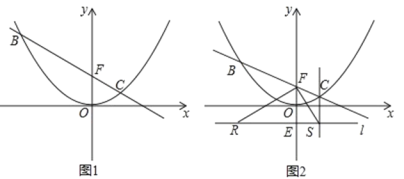
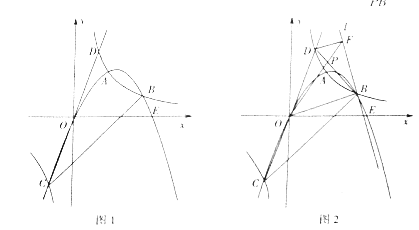
(1)如图 1,当点 C 的横坐标为 1 时,求直线 BC 的解析式;
(2)在(1)的条件下,点 M 是直线 BC 上一动点,过点 M 作 y 轴的平行线,与抛物线交于点 D, 是否存在这样的点 M,使得以 M、D、O、F 为顶点的四边形为平行四边形?若存在,求出点 M 的坐标;若不存在,请说明理由;
(3)如图 2,设 B(m,n)(m<0),过点 E(0,-1)的直线 l∥x 轴,BR⊥l 于 R,CS⊥l 于 S,连接 FR、FS.试判断△ RFS 的形状,并说明理由.
【答案】(1)![]() ;(2)存在;M点坐标为:(-3,
;(2)存在;M点坐标为:(-3,![]() ),
),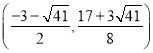 ,
,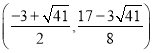 ;(3)△RFS是直角三角形;证明见详解.
;(3)△RFS是直角三角形;证明见详解.
【解析】
(1)首先求出C的坐标,然后由C、F两点用待定系数法求解析式即可;
(2)因为DM∥OF,要使以M、D、O、F为顶点的四边形为平行四边形,则DM=OF,设M(x,![]() ),则D(x,
),则D(x,![]() x2),表示出DM,分类讨论列方程求解;
x2),表示出DM,分类讨论列方程求解;
(3)根据勾股定理求出BR=BF,再由BR∥EF得到∠RFE=∠BFR,同理可得∠EFS=∠CFS,所以∠RFS=![]() ∠BFC=90°,所以△RFS是直角三角形.
∠BFC=90°,所以△RFS是直角三角形.
解:(1)因为点C在抛物线上,所以C(1,![]() ),
),
又∵直线BC过C、F两点,
故得方程组: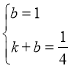
解之,得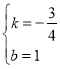 ,
,
所以直线BC的解析式为:![]() ;
;
(2)存在;理由如下:
要使以M、D、O、F为顶点的四边形为平行四边形,则MD=OF,如图1所示,
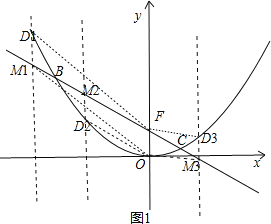
设M(x,![]() ),则D(x,
),则D(x,![]() x2),
x2),
∵MD∥y轴,
∴![]() ,
,
由MD=OF,可得:![]() ;
;
①当![]() 时,
时,
解得:x1=0(舍)或x1=-3,
所以M(-3,![]() );
);
②当![]() 时,
时,
解得:![]() ,
,
所以M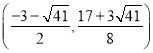 或M
或M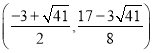 ,
,
综上所述,存在这样的点M,使以M、D、O、F为顶点的四边形为平行四边形,
M点坐标为:(-3,![]() ),
),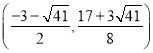 ,
,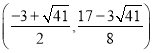 ;
;
(3)△RFS是直角三角形;理由如下:
过点F作FT⊥BR于点T,如图2所示,
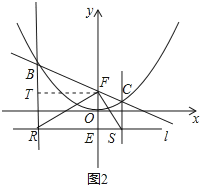
∵点B(m,n)在抛物线上,
∴m2=4n,
在Rt△BTF中,
![]()
![]()
![]()
![]() ,
,
∵n>0,
∴BF=n+1,
又∵BR=n+1,
∴BF=BR.
∴∠BRF=∠BFR,
又∵BR⊥l,EF⊥l,
∴BR∥EF,
∴∠BRF=∠RFE,
∴∠RFE=∠BFR,
同理可得∠EFS=∠CFS,
∴∠RFS=![]() ∠BFC=90°,
∠BFC=90°,
∴△RFS是直角三角形.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案