Question

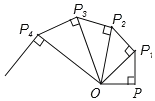
【题目】如图，OP=1，过P作PP1⊥OP，得OP1=；再过P1作P1P2⊥OP1且P1P2=1，得OP2=；又过P2作P2P3⊥OP2且P2P3=1，得OP3=2；…依次法继续作下去，S1，S2，S3…分别表示各个三角形的面积，那么S12+S22+S32+…+S92的值是（　　）

A.B.C.D.55

Answer 1

【答案】C

【解析】

先利用勾股定理推出OPn的规律，再求出每个图形的面积的平方和即可.

由勾股定理得：OP1=，OP2=；OP3=2；

OP4=；依此类推可得OPn=，

观察图形可知：第（n－1）个图形的斜边为第n个图形的直角边

∴Sn=OPn-1 ·Pn-1Pn=

∴S12=，S22=，S32=，…，S92=，∴S12+S22+S32+…+S92=．

故选C．