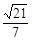题目内容
马航MH370失联后,我国政府积极参与搜救.某日,我两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50方向上,在救助船B的西北方向上,船B在船A正东方向140海里处。(参考数据:sin36.5≈0.6,cos36.5≈0.8,tan36.5≈0.75).
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处。
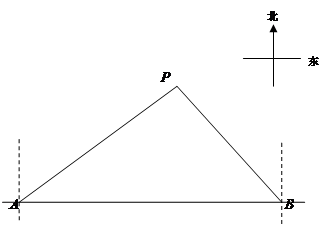
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处。
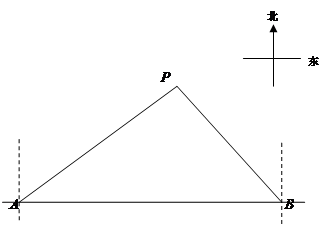
(1)可疑漂浮物P到A、B两船所在直线的距离为60海里.
(2)救助船A先到达P处.
(2)救助船A先到达P处.

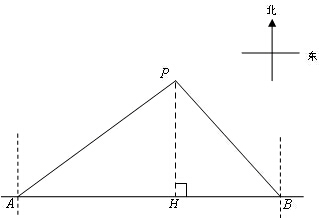
试题分析:(1)过点P作PH⊥AB于点H,在Rt△APH中解出PH即可;
(2)在Rt△BPH中,求出BP,分别计算出两艘船需要的时间,即可作出判断.
试题解析:(1)如图,过点P作PH⊥AB于点H,则PH的长是P到A、B两船所在直线的距离.
根据题意,得∠PAH=90°-53.50°=36.5°,∠PBH=45°,AB=140海里.
设PH=x海里
在Rt△PHB中,tan45°=
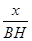 ,∴BH=x;
,∴BH=x;在Rt△PHA中,tan36.5°=
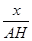 ,∴AH=
,∴AH= =
=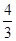 x.
x.∵AB=140,∴
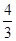 x +x=140,
x +x=140,解得x=60,即PH=60,因此可疑漂浮物P到A、B两船所在直线的距离为60海里.
在Rt△PHA中,AH=
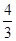 ×60=80, PA=
×60=80, PA=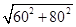 =100,
=100,救助船A到达P处的时间tA=100÷40=2.5小时;
在Rt△PHB中,PB=
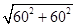 =60
=60 ,救助船B到达P处的时间tB=60
,救助船B到达P处的时间tB=60 ÷30=2
÷30=2 小时.
小时.∵2.5<2
 ,
,∴救助船A先到达P处.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
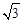 +2cos30°的值为 .
+2cos30°的值为 .



 和一个长为2、宽为1的长方形
和一个长为2、宽为1的长方形 拼在一起,构成一个大的长方形
拼在一起,构成一个大的长方形 .现将小长方形
.现将小长方形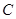 顺时针旋转至
顺时针旋转至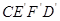 ,旋转角为
,旋转角为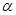 .
.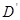 恰好落在
恰好落在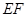 边上时,求旋转角
边上时,求旋转角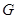 为
为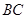 的中点,且0°<
的中点,且0°<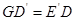 ;
;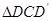 与
与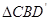 全等(0°<
全等(0°<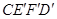 沿CD边竖直向上平移t个单位,设移动后小长方形边直线
沿CD边竖直向上平移t个单位,设移动后小长方形边直线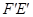 与BC交于点H,若DH∥FC,求上述运动变换过程中
与BC交于点H,若DH∥FC,求上述运动变换过程中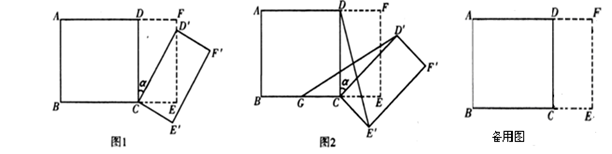

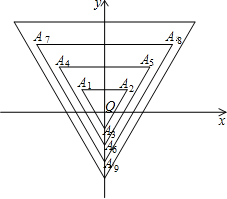
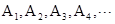 表示,其中x轴与边
表示,其中x轴与边 ,边
,边 ,
,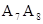 ,…均相距一个单位,则顶点
,…均相距一个单位,则顶点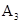 的坐标为 ;
的坐标为 ;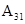 的坐标为 ;
的坐标为 ;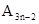 (n为正整数)的坐标为 .
(n为正整数)的坐标为 .