题目内容
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200﹣2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
【答案】(1)、当1≤x<50时,y==﹣2x2+180x+2000;当50≤x≤90时,y==﹣120x+12000;(2)、第45天时,当天销售利润最大,最大利润是6050元;(3)、41
【解析】
试题分析:(1)、根据单价乘以数量,可得利润,可得答案;(2)、根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;(3)、根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,根据解不等式组,可得答案.
试题解析:(1)、当1≤x<50时,y=(200﹣2x)(x+40﹣30)=﹣2x2+180x+2000, 当50≤x≤90时,
y=(200﹣2x)(90﹣30)=﹣120x+12000, 综上所述:y=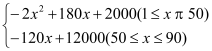 ;
;
(2)、当1≤x<50时,二次函数开口向下,二次函数对称轴为x=45, 当x=45时,y最大=﹣2×452+180×45+2000=6050, 当50≤x≤90时,y随x的增大而减小, 当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)、当1≤x<50时,y=﹣2x2+180x+2000≥4800,解得20≤x≤70, 因此利润不低于4800元的天数是20≤x<50,共30天; 当50≤x≤90时,y=﹣120x+12000≥4800,解得x≤60, 因此利润不低于4800元的天数是50≤x≤60,共11天, 所以该商品在销售过程中,共41天每天销售利润不低于4800元.