Question

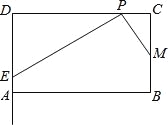
【题目】如图，在矩形ABCD中，AB=m，BC=4，点M为边BC的中点，点P为边CD上的动点（点P异于C，D两点）．连接PM，过点P作PM的垂线与射线DA相交于点E（如图）．

设CP=x，DE=y．

（1）求y与x之间的函数关系式；

（2）若点P在线段DC上运动时，点E总在线段AD上，求m的取值范围；

（3）当m=8时，是否存在点P，使得点D关于直线PE的对称点F落在边AB上？若存在，求x的值；若不存在，请说明理由．

Answer 1

【答案】(1)、y=﹣x2+mx；(2)、m≥4；(3)、x=2﹣

【解析】

试题分析：(1)、由△CPM∽△DEP得=由此即可解决问题．(2)、y=﹣x2+mx，根据函数的最大值是4，列出不等式即可解决问题．(3)、存在，过P作PH垂直于AB，由对称的性质得到：PD′=PD=8﹣x，ED′=ED=y=﹣x2+4x，EA=AD﹣ED=x2﹣4x+4，∠PD′E=∠D=90°，在Rt△D′PH中，PH=4，D′P=DP=8﹣x，根据勾股定理表示出D′H，再由△ED′A∽△D′PH，由相似得比例，将各自表示出的式子代入，可列出关于x的方程，求出方程的解即可得到满足题意的x的值．

试题解析：(1)、∵PE⊥PM，∴∠EPM=90°， ∴∠DPE+∠CPM=90°， 又矩形ABCD，∴∠D=90°，

∴∠DPE+∠DEP=90°， ∴∠CPM=∠DEP，又∠C=∠D=90°， ∴△CPM∽△DEP， ∴=，

又CP=x，DE=y，AB=DC=m，∴DP=m﹣x， 又M为BC中点，BC=4，∴CM=2， ∴=，∴y=﹣x2+mx．

(2)、由题意：﹣x2+mx≤4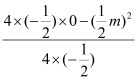， ∴≤4， ∴m2≥32， ∵m＞0 ∴m≥4．

(3)、存在，过P作PH⊥AB于点H，

∵点D关于直线PE的对称点D′落在边AB上， ∴PD′=PD=8﹣x，ED′=ED=y=﹣x2+4x，EA=AD﹣ED=x2﹣4x+4，∠PD′E=∠D=90°， 在Rt△D′PH中，PH=4，D′P=DP=8﹣x，

根据勾股定理得：D′H=，

∵∠ED′A=180°﹣90°﹣∠PD′H=90°﹣∠PD′H=∠D′PH，∠PD′E=∠PHD′=90°，

∴△ED′A∽△D′PH， ∴， 整理得：x2﹣4x+2=0，

解得：x=2±． 当x=2+时，y=5+2＞4，

此时，点E在边DA的延长线上，D关于直线PE的对称点不可能落在边AB上，所以舍去．

当x=2﹣时，y=5﹣2＜4，此时，点E在边AD上，符合题意．

所以当x=2﹣时，点D关于直线PE的对称点D′落在边AB上．