题目内容
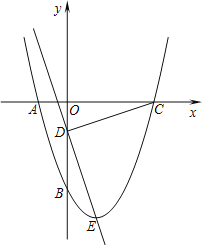
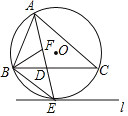
【题目】(1)问题发现:如图1,在四边形ABCD中,AB∥DC,E是BC的中点,若AE是∠BAD的平分线,则AB,AD,DC之间的数量关系为_______.
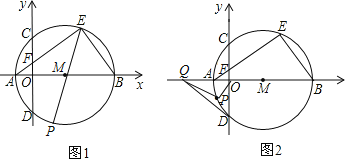
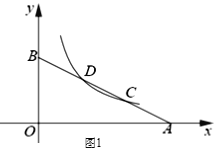
(2)问题探究:如图2,在四边形ABCD中,AB∥DC,E是BC的中点,点F是DC的延长线上一点,若AE是∠BAF的平分线,试探究AB,AF,CF之间的数量关系,并证明你的结论;
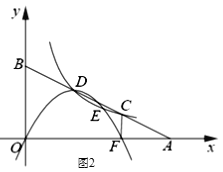
(3)问题解决:如图3,AB∥CD,点E在线段BC上,且BE:EC=3:4.点F在线段AE上,且∠EFD =∠EAB,直接写出AB,DF,CD之间的数量关系.

【答案】(1)AB+CD=AD;(2)详见解析;(3)AB=![]() (CD+DF ) .
(CD+DF ) .
【解析】
(1)结论:AB+CD=AD.只要证明△CEF≌△BEA(AAS),推出AB=CF,再证明DA=DF即可解决问题.
(2)结论:AB=AF+CF.只要证明△CEG≌△BEA(AAS),推出AB=CG,再证明FA=FG即可解决问题.
(3)结论:AB=![]() (CD+DF).如图3中,延长AE交CD的延长线于G.证明△CEG∽△BEA,推出AB=
(CD+DF).如图3中,延长AE交CD的延长线于G.证明△CEG∽△BEA,推出AB=![]() CG,再证明DF=DG即可解决问题.
CG,再证明DF=DG即可解决问题.
(1)结论:AB+CD=AD.
理由:如图1中,
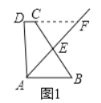
∵AB∥CF,∴∠CFE=∠EAB,
∵CE=EB,∠CEF=∠AEB,∴△CEF≌△BEA(AAS),
∴AB=CF.
∵AF平分∠DAB,∴∠DAF=∠EAB,
∵∠EAB=∠CFE,∴∠DAF=∠DFA,
∴AD=DF,
∵DF=DC+CF=CD+AB,
∴AB+CD=AD.
故答案为: AB+CD=AD.
(2)结论:AB=AF+CF
延长AE交DC的延长线于点G.
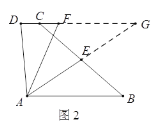
∵ AB∥CD, ∴ ∠EAB=∠G, ∠B=∠BCG.
又 E是BC的中点, ∴ BE=CE.
∴ △ABE≌△GCE,∴ AB=CG.
∵ AE是∠BAF的平分线,
∴ ∠EAB=∠FAE, ∴ ∠G=∠FAE.
∴ AF=FG, ∴ CG=CF+FG= CF+AF.
∴ AB=AF+CF.
(3)结论:AB=![]() (CD+DF ) .
(CD+DF ) .
如图3中,延长AE交CD的延长线于G.
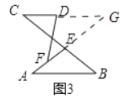
∵CG∥AB,
∴△CEG∽△BEA,
∴![]() ,
,
∵∠G=∠A,
∴AB=![]() CG,
CG,
∵∠DFE=∠A,
∴∠DFG=∠G,
∴DF=DG,
∴CD+DF=CD+DG=CG,
∴AB=![]() (CD+DF).
(CD+DF).

 应用题作业本系列答案
应用题作业本系列答案