题目内容
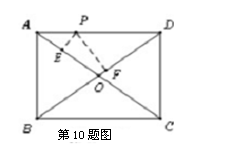
如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )
A.2.5 B.1.2 C.2.4 D.4.8

A.2.5 B.1.2 C.2.4 D.4.8
C
首先设未知线段为未知数,然后根据矩形的性质求出相似三角形,进而求解.
解:设PE=x,PF=a,PB=y.
由∠PBF=∠ABD,∠PFB=∠DAB可得△ABD∽△FBP,
故 =
= ,
,
同理可证 =
= ,
,
故a+x= ×3=
×3= .
.
故答案为C.
本题考查的是矩形的性质,要注意的是设线段的未知数,再进而证明相似三角形从而求解,难度中等.
解:设PE=x,PF=a,PB=y.
由∠PBF=∠ABD,∠PFB=∠DAB可得△ABD∽△FBP,
故
 =
= ,
,同理可证
 =
= ,
,故a+x=
 ×3=
×3= .
.故答案为C.
本题考查的是矩形的性质,要注意的是设线段的未知数,再进而证明相似三角形从而求解,难度中等.

练习册系列答案
相关题目
 中,
中, 为
为 上一点,且
上一点,且 .
. 为等腰直角三角形,斜边
为等腰直角三角形,斜边 与
与 交于点
交于点 ,延长
,延长 ,连接
,连接 、
、 ,作
,作 ,垂足为
,垂足为 ,下列结论:①
,下列结论:① ≌
≌ ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ ;⑤
;⑤ .其中正确的个数为( )
.其中正确的个数为( )

 ,
, ,坝高DE=6米.
,坝高DE=6米.
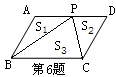
 A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2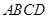 、正方形
、正方形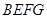 和正方形
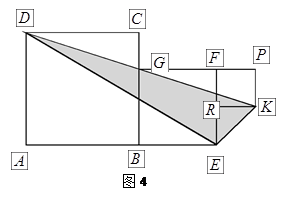
和正方形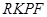 的位置如图4所示,点
的位置如图4所示,点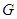 在线段
在线段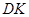 上,正方形
上,正方形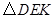 的面积为:
的面积为: