题目内容
如图，点P为□ABCD的边CD上一点，若△PAB、△PCD和△PBC的面积分别为
s1、s2和s3，则它们之间的大小关系是( )
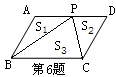
A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2
s1、s2和s3，则它们之间的大小关系是( )
A. S3=S1+S2 B. 2S3=S1+S2 C. S3>S1+S2 D. S3<S1+S2A
分析：设平行四边形的高为h，然后分别表示出s1、s2和s3，即可得出三者的关系．
解答：解：设平行四边形的高为h，
则S1=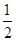
×AP×h，S2=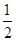PD×h，S3=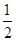BC×h，
又平心四边形的对边相等，
∴AP+PD=AD=BC，
∴S3=S1+S2．
故选A．
解答：解：设平行四边形的高为h，
则S1=
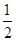×AP×h，S2=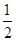PD×h，S3=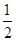BC×h，又平心四边形的对边相等，
∴AP+PD=AD=BC，
∴S3=S1+S2．
故选A．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
沿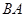
方向平移得到梯形
，
与
相交于点
，
=20cm，
=5cm，
=4cm，图中阴影部分的面积与哪个四边形的面积相等，并求出阴影部分的面积
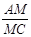的值是 ▲ . 
、
的正方形纸片和
的矩形纸片各若干块，试选用这些纸片（每种纸片至少用一次）在下面的虚线方框中拼成一个矩形（每两个纸片之间既不重叠，也无空隙，拼出的图中必须保留拼图的痕迹），使拼出的矩形面积为a2＋3ab＋2b2，并标出此矩形的长和宽．
