题目内容
【题目】探究:
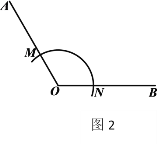
如图①,在△ABC中,点D、E、F分别在边AB、AC、CB上,且DE∥BC,EF∥AB,若∠ABC=65°,求∠DEF的度数.请将下面的解答过程补充完整,并填空(理由或数学式):

解:∵DE∥BC( )
∴∠DEF= ( )
∵EF∥AB
∴ =∠ABC( )
∴∠DEF=∠ABC( )
∵∠ABC=65°
∴∠DEF=
应用:
如图②,在△ABC中,点D、E、F分别在边AB、AC、BC的延长线上,且DE∥BC,EF∥AB,若∠ABC=β,则∠DEF的大小为 (用含β的代数式表示).
【答案】探究:见解析;应用:见解析.
【解析】
探究:依据两直线平行,内错角相等以及两直线平行,同位角相等,即可得到∠DEF=∠ABC,进而得出∠DEF的度数.应用:依据两直线平行,同位角相等以及两直线平行,同旁内角互补,即可得到∠DEF的度数.
解:探究:∵DE∥BC(已知)
∴∠DEF=∠CFE(两直线平行,内错角相等)
∵EF∥AB
∴∠CFE=∠ABC(两直线平行,同位角相等)
∴∠DEF=∠ABC(等量代换)
∵∠ABC=65°
∴∠DEF=65°
故答案为:已知;∠CFE;两直线平行,内错角相等;∠CFE;两直线平行,同位角相等;等量代换;65°.
应用:∵DE∥BC
∴∠ABC=∠D=β
∵EF∥AB
∴∠D+∠DEF=180°
∴∠DEF=180°﹣∠D=180°﹣β,
故答案为:180°﹣β.

练习册系列答案
相关题目