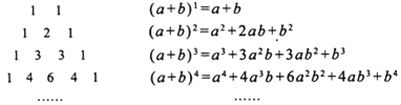题目内容
【题目】你能求（x﹣1）（x99+x98+x97+…+x+1）的值吗？遇到这样的问题，我们可以先思考一下，从简单的情形入手．先分别计算下列各式的值．
①（x﹣1）（x+1）＝x2﹣1
②（x﹣1）（x2+x+1）＝x3﹣1
③（x﹣1）（x3+x2+x+1）＝x4﹣1
……
由此我们可以得到：（x﹣1）（x99+x98+x97+…+x+1）＝
请你利用上面的结论，再完成下面两题的计算：
（1）（﹣2）50+（﹣2）49+（﹣2）48+…+（﹣2）+1
（2）若x3+x2+x+1＝0，求x2019的值
【答案】x100﹣1（1）
（2）﹣1
【解析】
先根据规律计算：（x﹣1）（x99+x98+x97+…+x+1）的结果；
（1）根据规律确定：x﹣1，就是﹣2﹣1，得原式＝（﹣2﹣1）
，根据公式可得结论；
（2）根据（x﹣1）（x3+x2+x+1）＝x4﹣1，代入已知可得x的值，根据x3+x2+x+1＝0，x2≥0，得x＜0，可得x＝﹣1，代入可得结论．
（1）由题意得：（x﹣1）（x99+x98+x97+…+x+1）＝x100﹣1，
故答案为：x100﹣1；
（1）（﹣2）50+（﹣2）49+（﹣2）48+…+（﹣2）+1，
＝（﹣2﹣1），
＝
，
＝；
（2）∵（x﹣1）（x3+x2+x+1）＝x4﹣1，x3+x2+x+1＝0，
∴x4＝1，
则x＝±1，
∵x3+x2+x+1＝0，
∴x＜0，
∴x＝﹣1，
∴x2019＝﹣1．
练习册系列答案
相关题目
