��Ŀ����
����Ŀ����֪���ڡ�ABC�У���BAC=90�㣬AB=AC����DΪֱ��BC��һ���㣨��D����B��C�غϣ�����ADΪ����������ADEF������CF��
��1����ͼ1������D���߶�BC��ʱ����֤��BD��CF��BD=CF��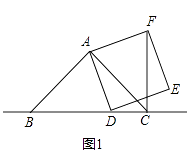
��2����ͼ2������D���߶�BC���ӳ�����ʱ�������������䣬�ڣ�1���ʽ��ۻ������𣿲�˵�����ɣ�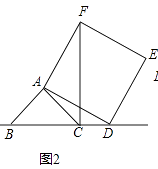
��3����ͼ3������D���߶�BC�ķ����ӳ�����ʱ���ҵ�A��F�ֱ���ֱ��BC�����࣬�����������䣺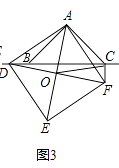
����ֱ��д��CF��BC��CD�����߶�֮��Ĺ�ϵ��
�������������ζԽ���AE��DF������ΪO������OC��̽����AOC����״����˵�����ɣ�
���𰸡�
��1��
֤�����ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
���ı���ADEF�������Σ�
��AD=AF����DAF=90�㣬
�ߡ�BAC=��BAD+��DAC=90�㣬��DAF=��CAF+��DAC=90�㣬
���BAD=��CAF��
�ڡ�BAD�͡�CAF�У� 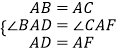
���BAD�ա�CAF��SAS����
��BD=CF����ACF=��ABD=45�㣬
���ACF+��ACB=90�㣬
��BD��CF��
��2��
��1���Ľ�����Ȼ���������ɣ�
�ߡ�BAD=��BAC+��CAD=90��+��CAD��
��CAF=��DAF+��CAD=90��+��CAD��
���BAD=��CAD��
�ڡ�BAD�͡�CAF�У� 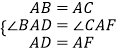
���BAD�ա�CAF��SAS����
��BD=CF����ACF=��ABD=45��
���BCF=��ACB+��ACF=45��+45��=90��
��BD��CF��
��3��
��BC��CD��CF�Ĺ�ϵ��CD=BC+CF
���ɣ��루1��ͬ����֤��BAD�ա�CAF���Ӷ��ɵã�
BD=CF��
����CD=BC+CF
�ڡ�AOC�ǵ���������
���ɣ��루1��ͬ����֤��BAD�ա�CAF���ɵã���DBA=��FCA��
�֡ߡ�BAC=90�㣬AB=AC��
���ABC=��ACB=45�㣬
���ABD=180�㩁45��=135�㣬
���ABD=��FCA=135��
���DCF=135�㩁45��=90��
���FCDΪֱ�������Σ�
�֡��ı���ADEF�������Σ��Խ���AE��DF�ཻ�ڵ�O��
��OC= ![]() DF��
DF��
��OC=OA
���AOC�ǵ���������
����������1���跨֤����BAD�ա�CAF���FCD=90�㼴�ɣ���2���루1��ͬ������3���еĢ��루1����ͬ����֤��BD=CF���ֵ�D��B��C���ߣ��ʣ�CD=BC+CF�����ɣ�1�����벢֤��BD��CF���Ӷ���֪��FCDΪֱ�������Σ����������εĶԽ��ߵ������ж���AOC���ߵ��ص㣬�ٽ�һ���ж�����״��
�����㾫����������Ҫ�����˵��������ε����ʵ����֪ʶ�㣬��Ҫ���յ��������ε���������ȣ���ƣ��ȱ߶ԵȽǣ�������ȷ�����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�