题目内容
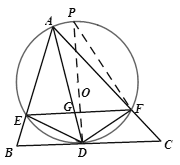
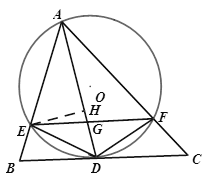
【题目】如图，AD是△ABC的角平分线，以AD为弦的⊙O交AB、AC于E、F，已知EF∥BC.
（1）求证：BC是⊙O的切线；
（2）若已知AE=9，CF=4，求DE长；
（3）在（2）的条件下，若∠BAC=60°，求tan∠AFE的值及GD长.
【答案】（1）证明见解析；（2）DE的长是6；
tan∠AFE的值为
，GD长为
【解析】（1）连接DO，并延长交⊙O于点P，
∵AD是△ABC的角平分线，
∴∠DAE=∠DAF，
∴
，
∴OD⊥EF，
∵EF∥BC，
∴OD⊥BC，D是半径OD的外端，
∴BC是⊙O的切线；
（2）∵DP是直径，
∴∠DFP=90°，
∴∠P+∠PDF=90°，
∵∠FDC+∠PDF=90°，
∴∠P=∠FDC=∠DAF=∠DAE，
∵四边形AEDF内接于圆，
∴∠AED=∠DFC，
∴△AED∽△DFC，
∴
，
∵
，
∴DE=DF，
∴DE2=AE×CF=9×4=36，
∴DE=6；
（3）如图，过E点作EH⊥AD于H点，
∵∠BAC=60°，
∴∠DAE=
∠BAC=30°，
∴EH=
AE=
，
由勾股定理得，AH=
，DH=
，
∴tan∠AFE=tan∠ADE=
；
AD=
+
∵
，
∴∠EAD=∠DEF，
又∠EDA=∠GDE，
∴△EDA∽△GDE，
∴
，
img src="//thumb.zyjl.cn/questionBank/Upload/2017/12/28/23/8a524687/SYS201712282305342279559724_DA/SYS201712282305342279559724_DA.018.png" width="189" height="67" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
