��Ŀ����
����Ŀ��Ϊ��չ���ξ��ã�����ij��������Ʊ���������Ʊ���������οͣ���Ʊ����Ϊ50Ԫ/�ˣ��ǽڼ��մ�a����Ʊ���ڼ��հ��Ŷ������ֶζ�����Ʊ����m�����£���m�ˣ����ŶӰ�ԭ����Ʊ������m�˵��Ŷӣ�����m����ԭ����Ʊ������m�˲��� ���οʹ�b����Ʊ����ij����������Ϊx�ˣ��ǽڼ��չ�Ʊ��Ϊy1��Ԫ�����ڼ��չ�Ʊ��Ϊy2��Ԫ����y1��y2֮��ĺ���ͼ����ͼ��ʾ��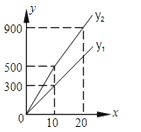
��1���۲�ͼ����a,b,m��ֵ
��2��ֱ��д��y1 �� y2��x֮��ĺ�����ϵʽ��
��3��ij�����絼��������5��1�մ�A�ţ�5��20�գ��ǽڼ��գ���B�Ŷ����þ������Σ�������Ʊ��1900Ԫ��A��B�����ŶӺϼ�50�ˣ���A��B�����ŶӸ��ж����ˣ�
���𰸡��⣺��1����Ʊ����Ϊ50Ԫ/�ˣ���ô10��Ӧ����500Ԫ������ͼ��֪ʵ��ֻ����300Ԫ���Ǵ�6�۵õ��ļ۸�
����a=6��
��ͼ��֪10��֮�����10�˻���400Ԫ����ԭ����500Ԫ������֪���Ǵ�8�۵õ��ļ۸�
����b=8��
��ͼ��֪m=10��
��2����y1=kx����x=10ʱ��y1=300���������еã�
k=30
y1�ĺ�����ϵʽΪ��y1=30x��
ͬ���ɵã�y2=50x��0��x��10����
��x��10ʱ���������ʽΪ��y2=kx+b��
���㣨10��500������20��900������ɵã�![]() ��
��
��ã�![]() ��
��
��y2=40x+100��
��y1��x֮��ĺ�����ϵʽΪ��y1=30x��y2��x֮��ĺ�����ϵʽΪ��y2=![]() ��
��
��3����A����n�ˣ���B���У�50��n���ˣ�
��0��n��10ʱ��50n+30��50��n��=1900��ã�
n=20����n��10ì�ܣ�
��n��10ʱ��40n+100+30��50��n��=1900��
��ã�n=30��50��30=20��
��A����30�ˣ�B����20�ˣ�
����������1������ԭƱ�ۺ�ʵ��Ʊ�ۿ���a��b��ֵ��m��ֵ�ɿ�ͼ�õ���
��2�����к�������ʽ��Ȼ��ͼ�еĶ�Ӧֵ�������������������ɵõ�����ʽ��
��3��������������ۣ���������10�Ͷ���10�ˣ��ҳ�������ϵ���г�����������n��һԪһ�η��̣���˿ɵ�������

����Ŀ��ijУ���꼶����150�����������������ȡ30�������ڡ�����������������ս��С��������ϡ����ԣ��±��Dz��Գɼ���¼����λ��������
3 | 2 | 1 | 2 | 3 | 3 | 5 | 2 | 2 | 4 |
2 | 4 | 2 | 5 | 2 | 3 | 4 | 4 | 1 | 3 |
3 | 2 | 5 | 1 | 4 | 2 | 3 | 1 | 2 | 4 |
��1�������Ѿ�����Ƶ���ֲ�����������ͳ��ͼ������ͳ��ͼ������ͳ��ͼ��Ϊ������������ʦһĿ��Ȼ֪�������������������ѡ��һ�ֺ��ʵ�ͳ�Ʊ���ͳ��ͼ������ʾ�������ݣ�
��2���۲������1���е�ͳ�Ʊ���ͳ��ͼ������д���������л�õ���Ϣ��
��3���涨���꼶�������������ϡ�4��������Ϊ�ϸ���ѧУ���ԡ��������ϡ����ϸ����������������飬�Թ���Ҫ���꼶�����������������飿

