题目内容
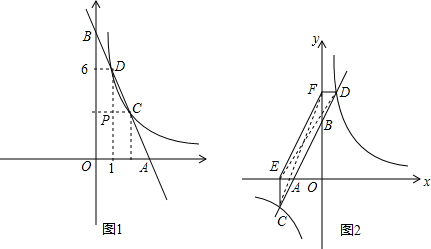
(2012•锡山区一模)已知:如图1,在平面直角坐标系中,O为坐标原点,直线y=kx+b与x轴、y轴分别交于点A、B,与双曲线y=
相交于C、D两点,且点D的坐标为(1,6).
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出
的值为
.
(2)如图2,当点A落在x 轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连接EF.
①判断△EFC的面积和△EFD的面积是否相等,并说明理由;
②当
=2时,求tan∠OAB的值.

| m |
| x |
(1)当点C的横坐标为2时,试求直线AB的解析式,并直接写出
| CD |
| AB |
| 1 |
| 3 |
| 1 |
| 3 |
(2)如图2,当点A落在x 轴的负半轴时,过点C作x轴的垂线,垂足为E,过点D作y轴的垂线,垂足为F,连接EF.
①判断△EFC的面积和△EFD的面积是否相等,并说明理由;
②当
| CD |
| AB |

分析:(1)由点D(1,6)在反比例函数y=
的图象上可求出m的值,进而得出反比例函数的解析式,再由点C的横坐标为2即可得出其纵坐标,故可得出C点坐标;
(2)①设C(a,b),则ab=6,由S△EFC=
(-a)(-b)=
ab=3,而S△EFD=
×1×6=3,故可得出结论;
②先由平行四边形的判定规定里定理得出四边形DFEA与四边形FBCE都是平行四边形,故可得出CE=BF,∠FDB=∠EAC,再由全等三角形的判定定理得出△DFB≌△AEC,故AC=BD,
=2,设CD=2k,AB=k,DB=
,故可得出
=
,再由△DFB∽△AOB,可知OA=2,且
=
,故可得出OB的长,进而得出结论.
| m |
| x |
(2)①设C(a,b),则ab=6,由S△EFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②先由平行四边形的判定规定里定理得出四边形DFEA与四边形FBCE都是平行四边形,故可得出CE=BF,∠FDB=∠EAC,再由全等三角形的判定定理得出△DFB≌△AEC,故AC=BD,
| CD |
| AB |
| k |
| 2 |
| DB |
| AB |
| 1 |
| 2 |
| BF |
| BO |
| 1 |
| 2 |
解答:解:(1)∵D(1,6)在y=
上,
∴m=6,即双曲线解析式是 y=
,
当C点横坐标为2时,纵坐标为3,
∴C(2,3).
直线AB过点C(2,3),D(1,6),得
,k=-3,b=9,
故直线AB的解析式为y=-3x+9;
的值为
;
(2)①设C(a,b),则ab=6,
∵S△EFC=
(-a)(-b)=
ab=3,而S△EFD=
×1×6=3,
∴S△EFC=S△EFD;
②∵S△EFC=S△EFD,且两三角形同底,
 ∴两三角形的高相同,
∴两三角形的高相同,
∴EF∥CD,
∵DF∥AE,BF∥CE,
∴四边形DFEA与四边形FBCE都是平行四边形,
∴CE=BF,∠FDB=∠EAC,
在△DFB与△AEC中,
∵
∴△DFB≌△AEC(ASA),
∴AC=BD,
∵
=2,设CD=2k,AB=k,DB=
,
∴
=
,
∵∠DFB=∠AOB,∠DBF=∠ABO,
∴△DFB∽△AOB,
∴OA=2,且
=
,
∴OB=4,
∴tan∠OAB=
=2.
| m |
| x |
∴m=6,即双曲线解析式是 y=
| 6 |
| x |
当C点横坐标为2时,纵坐标为3,
∴C(2,3).
直线AB过点C(2,3),D(1,6),得
|
故直线AB的解析式为y=-3x+9;
| CD |
| AB |
| 1 |
| 3 |
(2)①设C(a,b),则ab=6,
∵S△EFC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴S△EFC=S△EFD;
②∵S△EFC=S△EFD,且两三角形同底,
 ∴两三角形的高相同,
∴两三角形的高相同,∴EF∥CD,
∵DF∥AE,BF∥CE,
∴四边形DFEA与四边形FBCE都是平行四边形,
∴CE=BF,∠FDB=∠EAC,
在△DFB与△AEC中,
∵
|
∴△DFB≌△AEC(ASA),
∴AC=BD,
∵
| CD |
| AB |
| k |
| 2 |
∴
| DB |
| AB |
| 1 |
| 2 |
∵∠DFB=∠AOB,∠DBF=∠ABO,
∴△DFB∽△AOB,
∴OA=2,且
| BF |
| BO |
| 1 |
| 2 |
∴OB=4,
∴tan∠OAB=
| OB |
| OA |
点评:本题考查了反比例函数的综合运用,涉及待定系数法求函数解析式,同底等高的三角形的面积、相似三角形的性质等内容,综合性较强.

练习册系列答案
相关题目