题目内容
(2013•闸北区二模)已知:如图1,在梯形ABCD中,AD∥BC,∠A=90°,AD=6,AB=8,sinC=
,点P在射线DC上,点Q在射线AB上,且PQ⊥CD,设DP=x,BQ=y.
(1)求证:点D在线段BC的垂直平分线上;
(2)如图2,当点P在线段DC上,且点Q在线段AB上时,求y关于x的函数解析式,并写出定义域;
(3)若以点B为圆心、BQ为半径的⊙B与以点C为圆心、CP为半径的⊙C相切,求线段DP的长.

| 4 | 5 |
(1)求证:点D在线段BC的垂直平分线上;
(2)如图2,当点P在线段DC上,且点Q在线段AB上时,求y关于x的函数解析式,并写出定义域;
(3)若以点B为圆心、BQ为半径的⊙B与以点C为圆心、CP为半径的⊙C相切,求线段DP的长.

分析:(1)过D作DH⊥BC于H,得出四边形ABHD是矩形,推出DH=AB,BH=AD,在Rt△DHC中,求出DC=10,HC=6,推出BH=HC=6即可;
(2)延长BA、CD相交于点S,根据三角形的中位线求出SD=DC=10,SA=AB=8,得出DP=x,BQ=y,SP=x+10,证△SPQ~△SAD,得出
=
=
,求出SQ=
(x+10)即可;
(3)有三种情况:(ⅰ)当点P在线段DC上,且点Q在线段AB上时,只有可能两圆外切,由BQ+CP=BC,-
x+
+10-x=12,求出x即可;(ⅱ)当点P在线段DC上,且点Q在线段AB的延长线上时,两圆不可能相切,(ⅲ)当点P在线段DC的延长线上,且点Q在线段AB的延长线上时,得出BQ=
x-
,CP=x-10,若两圆外切,BQ+CP=BC,即
x-
+x-10=12,若两圆内切,|
x-
-(x-10)|=12,求出即可.
(2)延长BA、CD相交于点S,根据三角形的中位线求出SD=DC=10,SA=AB=8,得出DP=x,BQ=y,SP=x+10,证△SPQ~△SAD,得出
| SQ |
| SP |
| SD |
| SA |
| 5 |
| 4 |
| 5 |
| 4 |
(3)有三种情况:(ⅰ)当点P在线段DC上,且点Q在线段AB上时,只有可能两圆外切,由BQ+CP=BC,-
| 5 |
| 4 |
| 7 |
| 2 |
| 5 |
| 4 |
| 7 |
| 2 |
| 5 |
| 4 |
| 7 |
| 2 |
| 5 |
| 4 |
| 7 |
| 2 |
解答: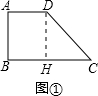 (1)证明:过D作DH⊥BC于H,如图①,
(1)证明:过D作DH⊥BC于H,如图①,
在梯形ABCD中,AD∥BC,∠A=90°,
∴∠B=∠A=90°,∠BHD=90°,
∴四边形ABHD是矩形,
∴DH=AB,BH=AD,
又∵AD=6,AB=8,
∴DH=8,BH=6,
在Rt△DHC中,sinC=
,设DH=4k=8,DC=5k
∴DC=10,HC=
=6,
∴BH=HC=6,
又∵DH⊥BC,
∴点D在线段BC的垂直平分线上.
(2)解:延长BA、CD相交于点S,如图②,
∵AD∥BC且BC=12,
∴AD=
BC,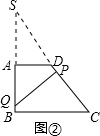
∴
=
=
=
,
∴SD=DC=10,SA=AB=8,
∵DP=x,BQ=y,SP=x+10,
∠S=∠S,∠SAD=∠SPQ=90°,
∴△SPQ~△SAD
∴
=
=
,
∴SQ=
(x+10),
∴BQ=16-
(x+10),
∴所求的解析式为:y=-
x+
,定义域是0≤x≤
.
(3)解:有三种情况:
(ⅰ)当点P在线段DC上,且点Q在线段AB上时,只有可能两圆外切,
由BQ+CP=BC,-
x+
+10-x=12,
解得:x=
,
(ⅱ)当点P在线段DC上,且点Q在线段AB的延长线上时,两圆不可能相切,
(ⅲ)当点P在线段DC的延长线上,且点Q在线段AB的延长线上时,
此时BQ=
x-
,CP=x-10
若两圆外切,BQ+CP=BC,即
x-
+x-10=12,
解得:x=
,
若两圆内切,|BQ-CP|=BC,
即|
x-
-(x-10)|=12,
x-
-(x-10)=12,
x-
-(x-10)=-12,
x=22,x=-74(不合题意舍去),
综上所述,⊙B与⊙C相切时,线段DP的长为
或
或22.
 (1)证明:过D作DH⊥BC于H,如图①,
(1)证明:过D作DH⊥BC于H,如图①,在梯形ABCD中,AD∥BC,∠A=90°,
∴∠B=∠A=90°,∠BHD=90°,
∴四边形ABHD是矩形,
∴DH=AB,BH=AD,
又∵AD=6,AB=8,
∴DH=8,BH=6,
在Rt△DHC中,sinC=
| 4 |
| 5 |
∴DC=10,HC=
| 102-82 |
∴BH=HC=6,
又∵DH⊥BC,
∴点D在线段BC的垂直平分线上.
(2)解:延长BA、CD相交于点S,如图②,
∵AD∥BC且BC=12,
∴AD=
| 1 |
| 2 |

∴
| SA |
| SB |
| SD |
| SC |
| AD |
| BC |
| 1 |
| 2 |
∴SD=DC=10,SA=AB=8,
∵DP=x,BQ=y,SP=x+10,
∠S=∠S,∠SAD=∠SPQ=90°,
∴△SPQ~△SAD
∴
| SQ |
| SP |
| SD |
| SA |
| 5 |
| 4 |
∴SQ=
| 5 |
| 4 |
∴BQ=16-
| 5 |
| 4 |
∴所求的解析式为:y=-
| 5 |
| 4 |
| 7 |
| 2 |
| 14 |
| 5 |
(3)解:有三种情况:
(ⅰ)当点P在线段DC上,且点Q在线段AB上时,只有可能两圆外切,
由BQ+CP=BC,-
| 5 |
| 4 |
| 7 |
| 2 |
解得:x=
| 2 |
| 3 |
(ⅱ)当点P在线段DC上,且点Q在线段AB的延长线上时,两圆不可能相切,
(ⅲ)当点P在线段DC的延长线上,且点Q在线段AB的延长线上时,
此时BQ=
| 5 |
| 4 |
| 7 |
| 2 |
若两圆外切,BQ+CP=BC,即
| 5 |
| 4 |
| 7 |
| 2 |
解得:x=
| 34 |
| 3 |
若两圆内切,|BQ-CP|=BC,
即|
| 5 |
| 4 |
| 7 |
| 2 |
| 5 |
| 4 |
| 7 |
| 2 |
| 5 |
| 4 |
| 7 |
| 2 |
x=22,x=-74(不合题意舍去),
综上所述,⊙B与⊙C相切时,线段DP的长为
| 2 |
| 3 |
| 34 |
| 3 |
点评:本题考查了圆与圆的位置关系,勾股定理,三角形的中位线,函数的应用等知识点的应用,主要考查学生综合运用性质进行推理和计算的能力,本题较好,有一定的难度.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 (2013•闸北区二模)某人在调查了本班同学的体重情况后,画出了频数分布图如图.下列结论中,不正确的是( )
(2013•闸北区二模)某人在调查了本班同学的体重情况后,画出了频数分布图如图.下列结论中,不正确的是( )