题目内容
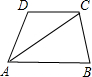在梯形ABCD中，AB∥DC，若∠D=120°，AD=DC，AC=AB，则∠B度数为
- A.75°
- B.60°
- C.65°
- D.85°
A
分析：根据已知条件，可推出∠B=∠4求解．
解答：
解：∵AB∥DC，
∴∠1=∠2，
又∵∠D=120°，AD=DC，
∴∠1=∠3=
（180°-∠D）=（180°-120°）=30°，
∴∠2=∠1=30°，
∵AC=AB，
∴∠B=∠4=（180°-∠2），
=（180°-30°），
=75°．
故选A．
点评：本题主要考查了平行线的性质及等腰三角形的性质，是基础题，比较简单．
分析：根据已知条件，可推出∠B=∠4求解．
解答：
解：∵AB∥DC，∴∠1=∠2，
又∵∠D=120°，AD=DC，
∴∠1=∠3=
（180°-∠D）=（180°-120°）=30°，∴∠2=∠1=30°，
∵AC=AB，
∴∠B=∠4=
（180°-∠2），=
（180°-30°），=75°．
故选A．
点评：本题主要考查了平行线的性质及等腰三角形的性质，是基础题，比较简单．
练习册系列答案
相关题目
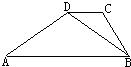10、如图，在梯形ABCD中，若AB∥CD，BD=AD，∠BCD=110°，∠CBD=30°，则∠ADC=
如图，在梯形ABCD中，AB∥CD，E是AB边上的点，给出下面三个论断：①AD=BC；②DE=CE；③AE=BE．请你以其中的两个论断为条件，填入“已知”栏中，以一个论断作为结论，填入“求证”栏中，使之成为一个正确的命题，并证明之．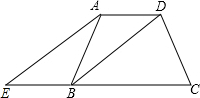
如图，在梯形ABCD中，AD∥BC，AD=AB，过点A作AE∥DB交CB的延长线于点E．
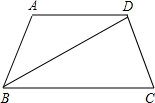如图，在梯形ABCD中，AD∥BC，AB=AD，BD=BC，∠A=100°，则∠BDC的度数为（ ）