题目内容
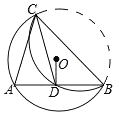
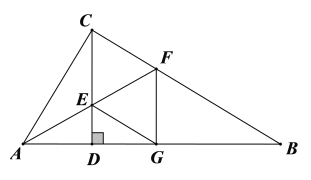
【题目】如图,在![]() 中,
中,![]() , 垂足为
, 垂足为![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)若![]() ,求
,求![]() 的长;
的长;
(2)过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]() ,试判断四边形
,试判断四边形![]() 的形状,并说明原因.
的形状,并说明原因.
【答案】(1)CE=2![]() ;(2)菱形,理由见解析.
;(2)菱形,理由见解析.
【解析】
(1)根据题意易求得∠ACD=∠CAF=∠BAF=30°,可得AE=CE,然后利用30°角的三角函数可求得CD的长、DE与AE的关系,进一步可得CE与CD的关系,进而可得结果;
(2)根据角平分线的性质可得CF=GF,根据HL可证Rt△ACF≌Rt△AGF,从而得∠AFC=∠AFG,由平行线的性质和等量代换可得∠CEF=∠CFE,可得CE=CF,进而得CE=FG,根据一组对边平行且相等可得四边形CEGF是平行四边形,进一步即得结论.
解:(1)∵∠ACB=90°,∠B=30°,∴∠CAB=60°,
∵CD⊥AB,∴∠ACD=30°,∵AC=6,∴![]() ,
,
∵AF平分∠CAB,∴∠CAF=∠BAF=30°,
∴∠ACD=∠CAF,![]() ,∴CE=AE=2DE,∴CE=
,∴CE=AE=2DE,∴CE=![]() 2
2![]() ;
;
(2)四边形CEGF是菱形.
证明:∵FG⊥AB,FC⊥AC,AF平分∠CAB,
∴∠ACF=∠AGF=90°,CF=GF,
在Rt△ACF与Rt△AGF中,∵AF=AF,CF=GF,
∴Rt△ACF≌Rt△AGF(HL),∴∠AFC=∠AFG,
∵CD⊥AB,FG⊥AB,∴CD∥FG,
∴∠CEF=∠EFG,∴∠CEF=∠CFE,∴CE=CF,
∴CE=FG,∵CE∥FG,
∴四边形CEGF是平行四边形,
∵CE=CF,∴平行四边形CEGF是菱形.


练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目