题目内容
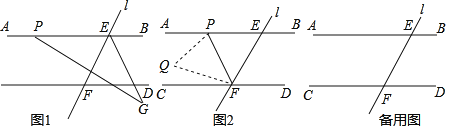
【题目】如图1，直线AB∥CD，直线l与直线AB，CD相交于点E，F，点P是射线EA上的一个动点（不包括端点）
（1）若∠CFE＝119°，PG交∠FEB的平分线EG于点G，∠APG＝150°，则∠G的大小为 ．
（2）如图2，连接PF．将△EPF折叠，顶点E落在点Q处．
①若∠PEF＝48°，点Q刚好落在其中的一条平行线上，请直接写出∠EFP的大小为 ．
②若∠PEF＝75°，∠CFQ＝
∠PFC，求∠EFP的度数．
【答案】（1）29.5°；（2）①42°或66°；②35°或63°．
【解析】
（1）根据平行线的性质和三角形的内角和即可得到结论；
（2）①Ⅰ、当点Q落在AB上时，利用三角形内角和定理计算即可．Ⅱ、当点Q落在CD上时，∠PQF＝∠PEF＝48°，利用平行线的性质，三角形的内角和定理计算即可．
②分两种情形：Ⅰ、当点Q在平行线AB，CD之间时．Ⅱ、当点Q在CD下方时，分别构建方程即可解决问题．
（1）∵直线AB∥CD，
∴∠BEF＝∠CFE＝119°，∠PEF＝180°﹣∠CFE＝61°，
∵EG平分∠BEF，
∴∠FEG＝
∠BEF＝59.5°，
∵∠APG＝150°，
∴∠EPF＝30°，
∴∠G＝180°﹣30°﹣61°﹣59.5°＝29.5°；
故答案为：29.5°；
（2）①Ⅰ、当点Q落在AB上时，
易证PF⊥AB，可得∠EPF＝90°，
∴∠EFP＝90°﹣∠PEF＝90°﹣48°＝42°．
Ⅱ、当点Q落在CD上时，∠PQF＝∠PEF＝48°，
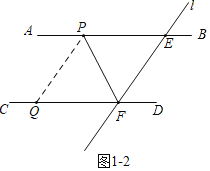
∵AB∥CD，
∴∠EPQ+∠PQF＝180°，
∴∠EPQ＝132°，
∵∠EPF＝∠QPF，
∴∠EPF＝×132°＝66°，
∴∠EFP＝180°﹣48°﹣66°＝66°．
综上所述，满足条件的∠EFP的值为42°或66°，
故答案为：42°或66°．
②Ⅰ、当点Q在平行线AB，CD之间时．
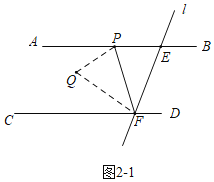
设∠PFQ＝x，由折叠可知∠EFP＝x，
∵2∠CFQ＝∠CFP，
∴∠PFQ＝∠CFQ＝x，
∴75°+3x＝180°，
∴x＝35°，
∴∠EFP＝35°．
Ⅱ、当点Q在CD下方时，
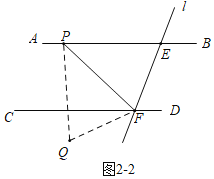
设∠PFQ＝x，由折叠可知∠EFP＝x，
∵2∠CFQ＝∠CFP，
∴∠PFC＝
x，
∴75°+x+x＝180°，
解得x＝63°，
∴∠EFP＝63°．
