Question

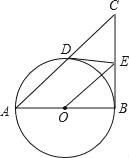
【题目】如图，在Rt△ABC中，∠ABC=90°，以AB为直径的⊙O与AC边交于点D，过点D作⊙O的切线交BC于点E，连接OE

(1)证明OE∥AD；

(2)①当∠BAC=　 　°时，四边形ODEB是正方形．

②当∠BAC=　 　°时，AD=3DE．

Answer 1

【答案】 (1)见解析 （2）①∠BAC=45°； ②当∠BAC=30°时，AD=3DE

【解析】

连接OD，根据已知条件易证Rt△ODE≌Rt△OBE得到∠BOE=∠DOB，根据圆周角定理可得∠A=∠DOB，即可得∠BOE=∠A，根据平行线的判定证明OE∥AD；（2）①根据正方形的性质和平行线的性质可得结论；②作OF⊥AD于F，根据垂径定理和锐角三角函数的知识计算即可得结论．

（1）连接OD，

∵DE是⊙O的切线，

∴OD⊥DE，

在Rt△ODE和Rt△OBE中，

，

∴Rt△ODE≌Rt△OBE，

∴∠BOE=∠DOB，

∵∠A=∠DOB，

∴∠BOE=∠A，

∴OE∥AD；

（2）①当四边形ODEB是正方形时，BO=BE，

∴∠BOE=45°，

∵OE∥AD，

∴∠BAC=45°；

②当∠BAC=30°时，AD=3DE，

证明：作OF⊥AD于F，

由垂径定理可知，AF=DF=AD，

∵∠BAC=30°，

∴∠ODF=∠DOE=30°，

∴OD==AD，

OD==DE，

∴AD=3DE．