题目内容
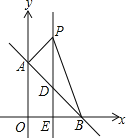
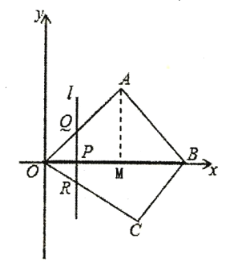
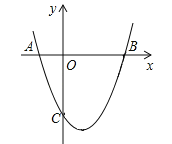
【题目】如图,抛物线与x轴的交点分别为A、B,与y轴的负半轴交于点C.已知抛物线的顶点坐标为(1,﹣4),点B的坐标(3,0).
(1)求该抛物线的解析式.
(2)在该函数图象上能否找到一点P,使PO=PC?若能,请求出点P的坐标;若不能,请说明理由.
【答案】(1) y=x2﹣2x﹣3;(2) 存在,P点坐标为(1+![]() ,﹣
,﹣![]() )或(1﹣
)或(1﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)可设出抛物线的顶点式,再利用B点坐标可求得抛物线解析式;
(2)由PO=PC可知点P在线段OC的垂直平分线上,则可知P点的纵坐标,代入抛物线解析式则可求得P点坐标.
(1)∵抛物线的顶点坐标为(1,﹣4),∴可设抛物线解析式为y=a(x﹣1)2﹣4.
∵抛物线过点B(3,0),∴0=a(3﹣1)2﹣4,解得:a=1,∴抛物线解析式为y=(x﹣1)2﹣4,即y=x2﹣2x﹣3;
(2)存在.
∵PO=PC,∴点P在线段OC的垂直平分线上,在y=x2﹣2x﹣3中,令x=0可得:y=﹣3,∴C(0,﹣3),∴P点纵坐标为﹣![]() ,在y=x2﹣2x﹣3中,令y=﹣
,在y=x2﹣2x﹣3中,令y=﹣![]() 可得:x2﹣2x﹣3=﹣
可得:x2﹣2x﹣3=﹣![]() ,解得:x=1±
,解得:x=1±![]() ,∴P点坐标为(1+
,∴P点坐标为(1+![]() ,﹣
,﹣![]() )或(1﹣
)或(1﹣![]() ,﹣
,﹣![]() ).
).

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】某城市为创建国家卫生城市,需要购买甲、乙两种类型的分类垃圾桶(如图所示),据调查该城市的A、B、C三个社区积极响应号并购买,具体购买的数和总价如表所示.
社区 | 甲型垃圾桶 | 乙型垃圾桶 | 总价 |
A | 10 | 8 | 3320 |
B | 5 | 9 | 2860 |
C | a | b | 2820 |
(1)运用本学期所学知识,列二元一次方程组求甲型垃圾桶、乙型垃圾桶的单价每套分别是多少元?
(2)按要求各个社区两种类型的垃圾桶都要有,则a= .