题目内容
【题目】已知:在△ABC外分别以AB,AC为边作△AEB与△AFC.
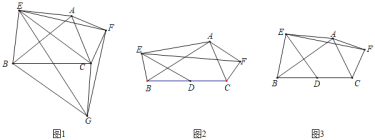
(1)如图1,△AEB与△AFC分别是以AB,AC为斜边的等腰直角三角形,连接EF.以EF为直角边构造Rt△EFG,且EF=FG,连接BG,CG,EC.
求证:①△AEF≌△CGF;②四边形BGCE是平行四边形.
(2)小明受到图1的启发做了进一步探究:
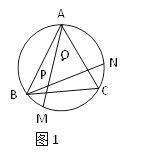
如图2,在△ABC外分别以AB,AC为斜边作Rt△AEB与Rt△AFC,并使∠FAC=∠EAB=30°,取BC的中点D,连接DE,EF后发现,两者间存在一定的数量关系且夹角度数一定,请你帮助小明求出![]() 的值及∠DEF的度数.
的值及∠DEF的度数.
(3)小颖受到启发也做了探究:
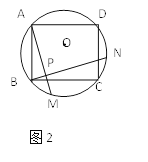
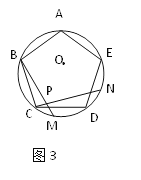
如图3,在△ABC外分别以AB,AC为底边作等腰三角形AEB和等腰三角形AFC,并使∠CAF+∠EAB=90°,取BC的中点D,连接DE,EF后发现,当给定∠EAB=α时,两者间也存在一定的数量关系且夹角度数一定,若AE=m,AB=n,请你帮助小颖用含m,n的代数式直接写出![]() 的值,并用含α的代数式直接表示∠DEF的度数.
的值,并用含α的代数式直接表示∠DEF的度数.
【答案】(1)①见解析;②见解析;(2)![]() =
=![]() ;(3)cos∠DEF=
;(3)cos∠DEF=![]() .
.
【解析】
(1)①根据SAS即可证明三角形全等.
②想办法证明BE=CG,BE∥CG即可.
(2)如图2中,延长ED到G,使得DG=ED,连接CG,FG.证明△CGF∽△AEF,推出![]() ,∠CFG=∠AFE,推出∠EFG=∠CFG+∠EFC=∠AFE+∠EFC=90°,推出tan∠DEF=
,∠CFG=∠AFE,推出∠EFG=∠CFG+∠EFC=∠AFE+∠EFC=90°,推出tan∠DEF=![]() ,可得∠DEF=30°即可解决问题.
,可得∠DEF=30°即可解决问题.
(3)如图3中,延长ED到G,使得DG=ED,连接CG,FG.作EH⊥AB于H,连接FD.想办法证明∠AEH=∠DEF,利用勾股定理求出EH,即可解决问题.
(1)证明:①如图1中,
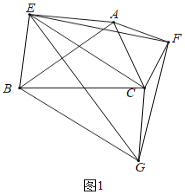
∵△EFC与△AFC都是等腰直角三角形,
∴FA=FC,FE=FG,∠AFC=∠EFG=90°,
∴∠AFE=∠CFG,
∴△AFE≌△CFG(SAS).
②∵△AFE≌△CFG,
∴AE=CG,∠AEF=∠CGF,
∵△AEB是等腰直角三角形,
∴AE=BE,∠BEA=90°,
∴CG=BE,
∵△EFG是等腰直角三角形,
∴∠FEG=∠FGE=45°,
∴∠AEF+∠BEG=45°,
∵∠CGE+∠CGF=45°,
∴∠BEG=∠CGE,
∴BE∥CG,
∴四边形BECG是平行四边形.
(2)解:如图2中,延长ED到G,使得DG=ED,连接CG,FG.
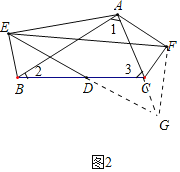
∵点D是BC的中点,
∴BD=CD,
∵∠EDB=∠GDC,
∴EB=GC,∠EBD=∠GCD,
在Rt△AEB与Rt△AFC中,
∵∠EAB=∠FAC=30°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵∠EBD=∠2+60°,
∴∠DCG=∠2+60°,
∴∠GCF=360°﹣60°﹣(∠2+60°)﹣∠3
=360°﹣120°﹣(∠2+∠3)
=360°﹣120°﹣(180°﹣∠1)
=60°+∠1,
∵∠EAF=30°+∠1+30°=60°+∠1,
∴∠GCF=∠EAF,
∴△CGF∽△AEF,
∴![]() ,∠CFG=∠AFE,
,∠CFG=∠AFE,
∴∠EFG=∠CFG+∠EFC=∠AFE+∠EFC=90°,
∴tan∠DEF=![]() ,
,
∴∠DEF=30°,
∴FG=![]() EG,
EG,
∵ED=![]() EG,
EG,
∴ED=FG,
∴![]() .
.
(3)如图3中,延长ED到G,使得DG=ED,连接CG,FG.作EH⊥AB于H,连接FD.
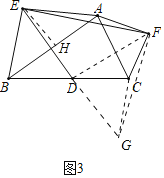
∵BD=DC,∠BDE=∠CDG,DE=DG,
∴△CDG≌△BDE(SAS),
∴CG=BE=AE,∠DCG=∠DBE=α+∠ABC,
∵∠GCF=360°﹣∠DCG﹣∠ACB﹣∠ACF=360°﹣(α+∠ABC)﹣∠ACB﹣(90°﹣α)=270°﹣(∠ABC+∠ACB)=270°﹣(180°﹣∠BAC)=90°+∠BAC=∠EAF,
∴△EAF≌△GCF(SAS),
∴EF=GF,∠AFE=∠CFG,
∴∠AFC=∠EFC,
∴∠DEF=∠CAF=90°﹣α,
∵∠AEH=90°﹣α,
∴∠AEH=∠DEF,
∵AE=m,AH=![]() AB=
AB=![]() n,
n,
∴EH=![]() ,
,
∵DE=DG,EF=GF,
∴DF⊥EG,
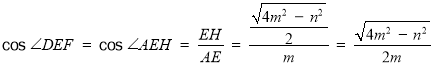 .
.

 阅读快车系列答案
阅读快车系列答案