��Ŀ����
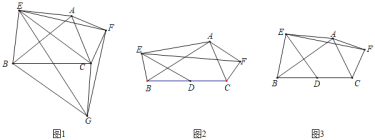
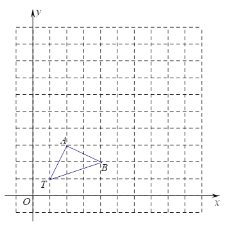
����Ŀ����ͼ����11��11�������������У���TAB�Ķ���ֱ�ΪT��1��1����A��2��3����B��4��2����
��1���Ե�T��1��1��Ϊλ�����ģ��������ߣ�TA����TA��3��1����λ�����ĵ�ͬ�ཫ��TAB�Ŵ�Ϊ��TA��B�����Ŵ���A��B�Ķ�Ӧ��ֱ�ΪA����B����������TA��B������д����A����B�������ꣻ��A��������Ϊ ����B��������Ϊ
��2���ڣ�1���У���C��a��b��Ϊ�߶�AB����һ�㣬д���仯���C�Ķ�Ӧ��C��������Ϊ ��
���𰸡���1��������;��2��C��(3a-2,3b-2).
��������
��1��������Ŀ����������λ�����ĵ�ͬ�ཫ��TAB�Ŵ�Ϊԭ����3�����õ���Ӧ�����꣬��ȷ������ͼ�μ��ɣ�����ͼ��ȷ����������꼴�ɣ�
��2�����ݣ�1���б任�Ĺ��ɣ�����д���仯���C�Ķ�Ӧ��C�������꣮
�⣺��1����ͼ��ʾ��
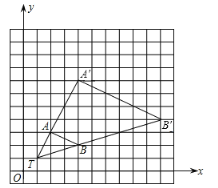
��A����B��������ֱ�Ϊ��A����4��7����B����10��4����
�ʴ�Ϊ��4��7��10��4��
��2���仯���C�Ķ�Ӧ��C��������Ϊ��C����3a-2��3b-2��
�ʴ�Ϊ��3a-2��3b-2��

��ϰ��ϵ�д�
 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
�����Ŀ