题目内容
【题目】已知一纸板的形状为正方形ABCD如图所示.其边长为10厘米,AD、BC与投影面β平行,AB、CD与投影面不平行,正方形在投影面β上的正投影为A1B1C1D1.若∠ABB1=45°,求投影面A1B1C1D1的面积.
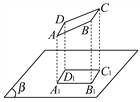
【答案】50![]() 平方厘米.
平方厘米.
【解析】试题分析:如图所示,过A作AH⊥BB1于H,由∠ABB1=45°可得△ABH是等腰直角三角形,结合cos45°可求出AH的长度,即求出A1B1的长度,又因为A1D1=AD,求出矩形A1B1C1D1的面积即可.
试题解析:
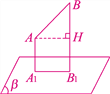
如图所示,过A作AH⊥BB1于H,
∵∠ABB1=45°,
∴△ABH是等腰直角三角形,
∴AH=AB·cos45°=10×![]() =5
=5![]() (厘米),
(厘米),
∴A1B1=AH=5![]() (厘米),
(厘米),
∵A1D1=AD=10(厘米),
∴矩形A1B1C1D1的面积=A1B1·A1D1=5![]() ×10=50
×10=50![]() (平方厘米).
(平方厘米).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目