题目内容
【题目】已知半径为10的⊙O中,弦![]() ,弦AC=10,则∠BAC的度数是为________
,弦AC=10,则∠BAC的度数是为________
【答案】15°或105°
【解析】
根据点O与∠BAC的位置分类讨论,分别画出对应的图形,利用勾股定理的逆定理和等边三角形的性质分别求出∠OAB和∠OAC,即可求出∠BAC的度数.
解:若点O在∠BAC的内部,如下图所示,连接OB、OA和OC
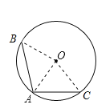
∴OA=OB=OC=10
∵弦![]() ,弦AC=10,
,弦AC=10,
∴OB2+OA2=200=AB2,OA=AC=OC
∴△OAB为等腰直角三角形,△OAC为等边三角形
∴∠OAB=45°,∠OAC=60°
∴∠BAC=∠OAB+∠OAC=105°;
若点O不在∠BAC的内部,如下图所示,连接OB、OA和OC
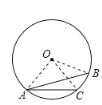
∴OA=OB=OC=10
∵弦![]() ,弦AC=10,
,弦AC=10,
∴OB2+OA2=200=AB2,OA=AC=OC
∴△OAB为等腰直角三角形,△OAC为等边三角形
∴∠OAB=45°,∠OAC=60°
∴∠BAC=∠OAC-∠OAB=15°;
综上所述:∠BAC=15°或105°
故答案为:15°或105°.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
【题目】某文具店每天售出甲、乙两种笔,统计后发现:甲、乙两种笔同一天售出量之间满足一次函数的关系,设甲、乙两种笔同一天的售出量分别为x(支)、y(支),部分数据如表所示(下表中每一列数据表示甲、乙两种笔同一天的售出量).
甲种笔售出x(支) | … | 4 | 6 | 8 | … |
乙种笔售出y(支) | … | 6 | 12 | 18 | … |
(1)求y关于x的函数关系式;(不需要写出函数的定义域)
(2)某一天文具店售出甲、乙两种笔的营业额分别为30元和120元,如果乙种笔每支售价比甲种笔每支售价多2元,那么甲、乙两种笔这天各售出多少支?