题目内容
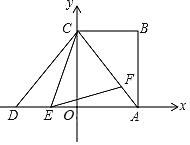
【题目】已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，且关于x的一元二次方程ax2+bx+c﹣m＝0没有实数根，则下列结论：①b2﹣4ac＞0；②ac＜0；③m＞2，其中正确结论的个数是（ ）
A.0B.1C.2D.3
【答案】D
【解析】
根据函数图象和二次函数的性质可以判断题目中的各个小题是否成立，从而可以解答本题．
解：由二次函数y＝ax2+bx+c（a≠0）的图象与x轴两个交点，可得b2﹣4ac＞0，故①正确，
由二次函数y＝ax2+bx+c（a≠0）的图象可知a＜0，c＞0，则ac＜0，故②正确，
由二次函数y＝ax2+bx+c（a≠0）的图象可知该函数有最大值，最大值是y＝2，
∵关于x的一元二次方程ax2+bx+c﹣m＝0没有实数根，则m＞2，故③正确，
故选：D．
练习册系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀，让学生进行摸球试验，每次摸出一个球（放回），下表是活动进行中的一组统计数据．
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
|
（1）
= ，根据上表数据估计从袋中摸出一个黑球的概率是 ．
（2）估算袋中白球的个数为 ．
（3）在（2）的条件下，若小强同学从袋中摸出两个球，用画树状图或列表的方法计算摸出的两个球都是白球的概率．