Question

【题目】在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积． 某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．
作AD⊥BC于D，设BD=x，用含x的代数式表示CD→根据勾股定理，利用AD作为“桥梁”，建立方程模型求出x→利用勾股定理求出AD的长，再计算三角形的面积．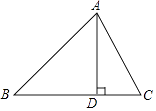

Answer 1

【答案】解：如图，在△ABC中，AB=15，BC=14，AC=13， 设BD=x，则有CD=14﹣x，
由勾股定理得：AD2=AB2﹣BD2=152﹣x2 ， AD2=AC2﹣CD2=132﹣（14﹣x）2 ，
∴152﹣x2=132﹣（14﹣x）2 ，
解之得：x=9，
∴AD=12，
∴S△ABC= BCAD= ×14×12=84
【解析】设BD=x，由CD=BC﹣BD表示出CD，分别在直角三角形ABD与直角三角形ACD中，利用勾股定理表示出AD2 ， 列出关于x的方程，求出方程的解得到AD的长，即可求出三角形ABC面积．