题目内容
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
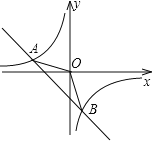
(1)求一次函数和反比例函数的解析式;
(2)观察图象,直接写出不等式kx+b﹣![]() <0的解集.
<0的解集.
(3)P是x轴上的一点,且满足△APB的面积是9,写出P点的坐标。
【答案】(1)反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣x﹣2;
,一次函数的解析式为y=﹣x﹣2;
(2)不等式解集为﹣4<x<0或x>2;
(3)点P坐标为(-5,0),或(1,0)
【解析】试题分析:对于(1),由A(-4,n),B(2,4)是一次函数y=kx+b和反比例函数y=![]() 的图象的两个交点,利用待定系数法分别求出一次函数y=kx+b和反比例函数y= y=
的图象的两个交点,利用待定系数法分别求出一次函数y=kx+b和反比例函数y= y=![]() ;
;
对于(2),根据图象的增减性可直接得到答案.
对于(3)由S△APB=S△ACP+S△BPC可得PC=3,点C的坐标为(﹣2,0),点P 分在C点左侧和右侧两种情况求坐标.
试题解析:(1)∵B(2,﹣4)在y= y=![]() 上,
上,
∴m=﹣8.
∴反比例函数的解析式为y=﹣![]() .
.
∵点A(﹣4,n)在y=﹣![]() 上,
上,
∴n=2.
∴A(﹣4,2).
∵y=kx+b经过A(﹣4,2),B(2,﹣4),
∴![]() ,解得:
,解得: ![]() .
.
∴一次函数的解析式为y=﹣x﹣2.
(2)不等式kx+b﹣y=![]() <0的解集为﹣4<x<0或x>2.
<0的解集为﹣4<x<0或x>2.
(3)∵S△APB=S△ACP+S△BPC
∴![]()
∴PC=3
∵y=0时,x=﹣2.∴点C(﹣2,0).
当P在C点的左侧时,P1(-5,0),当P在C点的右侧时,P2(1,0)

练习册系列答案
相关题目