题目内容
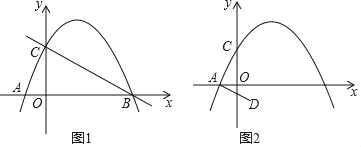
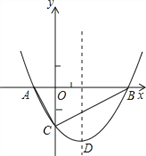
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,且
点,且![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与![]() 轴另一个交点
轴另一个交点![]() 的坐标,并观察图象直接写出当
的坐标,并观察图象直接写出当![]() 为何值时
为何值时![]() ?
?
【答案】(1)抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣2;(2)B点坐标为(4,0),x<﹣1或x>4.
x﹣2;(2)B点坐标为(4,0),x<﹣1或x>4.
【解析】试题分析:把A(﹣1,0)代入y=![]() x2+bx﹣2得b=-
x2+bx﹣2得b=-![]() ,即可得解;
,即可得解;
(2)令y=0,得方程x2﹣3x﹣4=0,求得x 的值,即可得B点坐标,观察图象得出当![]() 为何值时
为何值时![]() .
.
试题解析:(1)把A(﹣1,0)代入y=![]() x2+bx﹣2得
x2+bx﹣2得![]() ﹣b﹣2=0,解得b=﹣
﹣b﹣2=0,解得b=﹣![]() ,
,
所以抛物线解析式为y=![]() x2﹣
x2﹣![]() x﹣2,
x﹣2,
(2)当y=0时, ![]() x2﹣
x2﹣![]() x﹣2=0,
x﹣2=0,
整理得x2﹣3x﹣4=0,解得x1=﹣1,x2=4,
所以B点坐标为(4,0),
观察图象,得:当x<﹣1或x>4时,y>0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |

请根据以上信息解答下列问题:
(1)填空:m= ______ ,n= ______ ;
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在______ 组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.