Question

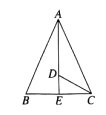
【题目】如图，在△ABC中，已知AB＝AC，∠BAC和∠ACB的平分线相交于点D，∠ADC＝125°，求∠ACB和∠BAC的度数．

Answer 1

【答案】∠ACB＝70°；∠BAC＝40°.

【解析】试题分析:根据等腰三角形三线合一的性质可得AE⊥BC，再求出∠CDE，然后根据直角三角形两锐角互余求出∠DCE，根据角平分线的定义求出∠ACB，再根据等腰三角形两底角相等列式进行计算即可求出∠BAC．

试题解析：∵AB=AC，AE平分∠BAC，

∴AE⊥BC（等腰三角形三线合一），

∵∠ADC=125°，

∴∠CDE=55°，

∴∠DCE=90°﹣∠CDE=35°，

又∵CD平分∠ACB，

∴∠ACB=2∠DCE=70°，

又∵AB=AC，

∴∠B=∠ACB=70°，

∴∠BAC=180﹣（∠B+∠ACB）=40°．