题目内容
【题目】已知:抛物线y=﹣![]() x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2)
x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2)
(1)求抛物线的表达式;
(2)点P为第一象限抛物线上一点,是否存在使△PBC面积最大的点P?若不存在,请说明理由;若存在,求出点P的坐标;
(3)点D坐标为(1,﹣1),连接AD,将线段AD绕平面内某一点旋转180度得线段MN(点M、N分别与点A、D对应),使点M、N都在抛物线上,求点M、N的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)当x=2时,S有最大值为4,此时P(2,3);(3)N(1,3),M(3,2).
x+2;(2)当x=2时,S有最大值为4,此时P(2,3);(3)N(1,3),M(3,2).
【解析】
(1) 根据抛物线y=y=﹣![]() x2+bx+c经过A (-1, 0)C(0,2)两点,列出b和c的二元一次方程组,求出b和c的值, 进而求出抛物线的表达式;
x2+bx+c经过A (-1, 0)C(0,2)两点,列出b和c的二元一次方程组,求出b和c的值, 进而求出抛物线的表达式;
(2)过点P作PQ//y轴,交直线BC于Q,设P(x,![]() ),则Q(x,
),则Q(x,![]() );求出PQ的长, 利用
);求出PQ的长, 利用![]() =
=![]() PQ.OB列出S关于的二次函数, 利用函数的性质求出面积的最大值,进而求出点P的坐标;
PQ.OB列出S关于的二次函数, 利用函数的性质求出面积的最大值,进而求出点P的坐标;
(3)作辅助线,根据线段AD绕平面内某一点旋转180度得线段MN可知: 旋转后的MN与AD平行且相等,构建全等三角形:ΔADG≌ΔMNG,根据A、 D两点的坐标发现, N点向下平移1个单位再向右移动两个单位得M,设N的坐标为:设N(m,![]() ) , 根据平移规律表示M (m+2,
) , 根据平移规律表示M (m+2, ![]() ) , 代入抛物线的解析式即可
) , 代入抛物线的解析式即可
(1)∵抛物线y=﹣![]() x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2),
x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2),
∴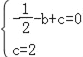 ,
,
解得![]() ,
,
∴抛物线的解析式:y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵令y=0,则=﹣![]() x2+
x2+![]() x+2=0,
x+2=0,
解得x1=﹣1,x2=4
∴B(4,0),
∴直线BC:y=﹣![]() x+2;
x+2;
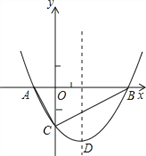
如图1,过点P作PQ∥y轴,交直线BC于Q,
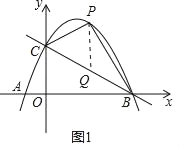
设P(x,﹣![]() x2+
x2+![]() x+2),则Q(x,﹣
x+2),则Q(x,﹣![]() x+2);
x+2);
∴PQ=(﹣![]() x2+
x2+![]() x+2)﹣(﹣
x+2)﹣(﹣![]() x+2)=﹣
x+2)=﹣![]() x2+2x,
x2+2x,
S△PCB=![]() PQOB=
PQOB=![]() ×(﹣
×(﹣![]() x2+2x)×4=﹣(x﹣2)2+4;
x2+2x)×4=﹣(x﹣2)2+4;
当x=2时,S有最大值为4,此时P(2,3);
(3)如图2,过D作DG⊥x轴于G,过N作NH∥y轴,过M作MH∥x轴,交于H,

由题意得:△ADG≌△MNG,
∵A(﹣1,0),D(1,﹣1),
∴AG=2,DG=1,
∴NH=DG=1,MH=AG=2,
设N(m,﹣![]() m2+
m2+![]() m+2),则M(m+2,﹣
m+2),则M(m+2,﹣![]() m2+
m2+![]() m+2﹣1),
m+2﹣1),
把M的坐标代入抛物线y=﹣![]() x2+
x2+![]() x+2中得:
x+2中得:
﹣![]() (m+2)2+
(m+2)2+![]() (m+2)+2=﹣
(m+2)+2=﹣![]() m2+
m2+![]() m+2﹣1,
m+2﹣1,
解得:m=1,
当m=1时,﹣![]() m2+
m2+![]() m+2=3,
m+2=3,
∴N(1,3),M(3,2).

 名校课堂系列答案
名校课堂系列答案