Question

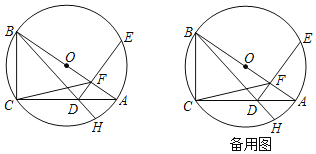
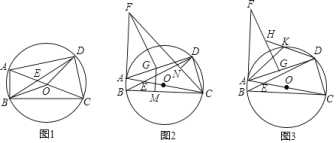
【题目】已知，四边形ABCD内接于，对角线AC和BD相交于点E，AC是的直径．

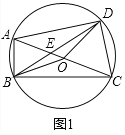
如图1，连接OB和OD，求证：；

如图2，延长BA到点F，使，在AD上取一点G，使，连接FG和FC，过点G作，垂足为M，过点D作，垂足为N，求的值；

如图3，在的条件下，点H为FG的中点，连接DH交于点K，连接AK，若，，求线段BC的长．

Answer 1

【答案】（1）证明见解析；（2）；（3） .

【解析】

(1)利用圆周角定理得到∠AOB=2∠ACB，∠COD=2∠DBC，得用三角形的外角定理得到∠ACB+∠DBC=∠AEB，从而得到结论；

(2)连接GC，先证明∠MCG=∠NCD，得到；

(3)先证≌，再证≌，设PQ=a，PD=7a，可求出QD=a，RQ=a，利用三角函数关系即可求解.

证明：如图1中，

，

，

，

，

，

，

．

如图2中，连接GC．

是直径，

，

，

，，

，，

，

，

．

如图3中，延长DH到T，使得，连接TF，TB，CK，作于P交AD于点Q，作于R．

点H是FG的中点，

，

，，

≌，

，，

，，

，

，，

，

，

，

≌，

，，

，

，

是等腰直角三角形，

，

，设，，

在中，可得，

，

，

在中，，

在中，，

，

，

在中，，

，

，

，

，

，设，，则，

，

．

故答案为：(1)证明见解析；(2)；(3).