题目内容
【题目】反比例函数![]() 在第一象限上有两点A,B.
在第一象限上有两点A,B.
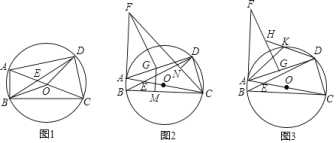
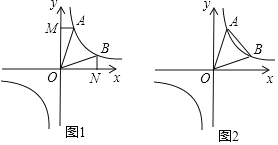
(1)如图1,AM⊥y轴于M,BN⊥x轴于N,求证:△AMO的面积与△BNO面积相等;
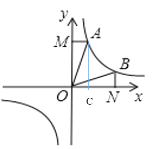
(2)如图2,若点A(2,m),B(n,2)且△AOB的面积为16,求k值.
【答案】(1)见解析;(2)12.
【解析】
(1)根据反比例函数的k值的含义即可证明,
(2)过点A作AC⊥x轴,则AM=2,AC=m,BN=2,CN=n-2,根据S△AOB=S四边形ACOM+S梯形ACBN-S△AOM-S△BON,列出其面积的表示式子又m=n,即可化简得![]() ,得m=6,故求出k值
,得m=6,故求出k值
(1)设某点A(x1,y1),B(x2,y2)
∵A,B都在反比例函数![]() 上,
上,
∴x1y1=x2y2,
∴S△AMO=![]() x1y1=S△BNO=
x1y1=S△BNO=![]() x2y2
x2y2
即△AMO的面积与△BNO面积相等;
(2)过点A作AC⊥x轴,
则AM=2,AC=m,BN=2,CN=n-2,
S△AOB=S四边形ACOM+S梯形ACBN-S△AOM-S△BON,
即16=2m+![]() (2+m)(n-2)-
(2+m)(n-2)-![]() ×2×2m
×2×2m
∵m=n
∴可化简为![]() ,
,
∴m=6,(-6舍去)
∴k=2m=12.

练习册系列答案
相关题目