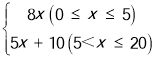题目内容
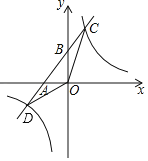
【题目】如图，二次函数
的图象与
轴交于点
(点
位于对称轴的左侧)，与
轴交于点
.已知
．
求该二次函数的对称轴及点
的坐标．
点
为线段
上一点,过点
作直线
轴交图象于点
(点
在点
的左侧),将顶点
作直线
的对称点
，若点在轴上方，且到轴距离为1，求
的值．
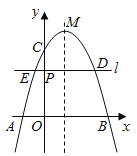
【答案】
对称轴直线x=1；B(3，0)；
n=
【解析】
(1)根据OA=1，得出A点坐标，根据待定系数法把A点坐标带入二次函数解析式，从而求出a的值，求出二次函数解析式，根据对称轴公式求出对称轴；令y等于0，可求出B点坐标．
（2）根据函数解析式求出顶点M的坐标，利用条件M，M1关于直线l对称，且M1到
轴距离为1，求出M1的坐标，进而可求出n的值．
解：∵OA=1
∴A(﹣1,0)
把
代入
得
∴
∴对称轴
令
，即
解得
∴
∴顶点
关于垂线
对称，且到x轴距离为1
则
∴
．
练习册系列答案
相关题目
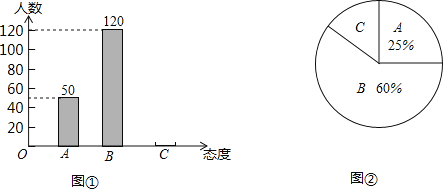
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛，赛后随机抽取了各年级部分学生成绩进行统计，制作如下频数分布表和频数分布直方图．请根据图表中提供的信息，解答下列问题：
分数段（ | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
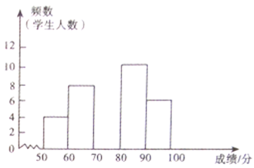
（1）请求出该校随机抽取了____学生成绩进行统计；
（2）表中
____，
____，并补全直方图；
（3）若用扇形统计图描述此成绩统计分布情况，则分数段
对应扇形的圆心角度数是___
；
（4）若该校共有学生8000人，请估计该校分数在
的学生有多少人？
