Question

【题目】如图，⊙O的直径AC与弦BD相交于点F，点E是DB延长线上的一点，∠EAB=∠ADB．
（1）求证：EA是⊙O的切线；
（2）已知点B是EF的中点，求证：以A、B、C为顶点的三角形与△AEF相似；
（3）已知AF=4，CF=2．在（2）条件下，求AE的长．

Answer 1

【答案】
（1）证明：如图1，连接CD，

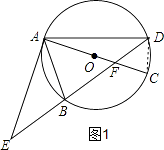
∵AC是⊙O的直径，

∴∠ADC=90°，

∴∠ADB+∠EDC=90°，

∵∠BAC=∠EDC，∠EAB=∠ADB，

∴∠EAC=∠EAB+∠BAC=90°，

∴EA是⊙O的切线．

（2）证明：如图2，连接BC，

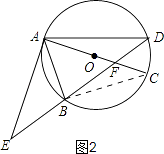
∵AC是⊙O的直径，

∴∠ABC=90°，

∴∠CBA=∠ABC=90°

∵B是EF的中点，

∴在RT△EAF中，AB=BF，

∴∠BAC=∠AFE，

∴△EAF∽△CBA．

（3）解：∵△EAF∽△CBA，

∴ = ，

∵AF=4，CF=2．

∴AC=6，EF=2AB，

∴ = ，解得AB=2 ．

∴EF=4 ，

∴AE= = =4 ，

【解析】（1）连接CD，由AC是⊙O的直径，可得出∠ADC=90°，由角的关系可得出∠EAC=90°，即得出EA是⊙O的切线，（2）连接BC，由AC是⊙O的直径，可得出∠ABC=90°，由在RT△EAF中，B是EF的中点，可得出∠BAC=∠AFE，即可得出△EAF∽△CBA，（3）由△EAF∽△CBA，可得出 = ，由比例式可求出AB，由勾股定理得出AE的长．
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识，掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．