ЬтФПФкШн
ЁОЬтФПЁПШчЭМЂйХзЮяЯпyЃНax2+bx+4ЃЈaЁй0ЃЉгыxжсЃЌyжсЗжБ№НЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌЕуCШ§ЕуЃЎ
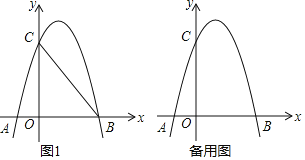
ЃЈ1ЃЉЪдЧѓХзЮяЯпЕФНтЮіЪНЃЛ
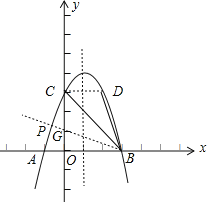
ЃЈ2ЃЉЕуDЃЈ3ЃЌmЃЉдкЕквЛЯѓЯоЕФХзЮяЯпЩЯЃЌСЌНгBCЃЌBDЃЎЪдЮЪЃЌдкЖдГЦжсзѓВрЕФХзЮяЯпЩЯЪЧЗёДцдквЛЕуPЃЌТњзуЁЯPBCЃНЁЯDBCЃПШчЙћДцдкЃЌЧыЧѓГіЕуPЕуЕФзјБъЃЛШчЙћВЛДцдкЃЌЧыЫЕУїРэгЩЃЛ
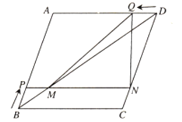
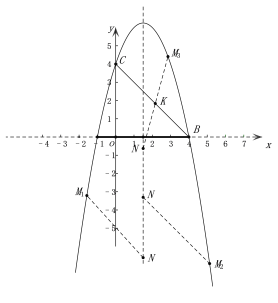
ЃЈ3ЃЉЕуNдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЕуMдкХзЮяЯпЩЯЃЌЕБвдMЁЂNЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+3x+4ЃЛЃЈ2ЃЉДцдкЃЎPЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎЃЈ3ЃЉ
ЃЉЃЎЃЈ3ЃЉ![]()
![]()
![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋA,B,CШ§ЕуДњШыyЃНax2+bx+4ЧѓГіa,b,cжЕЃЌМДПЩШЗЖЈБэДяЪНЃЛ
ЃЈ2ЃЉдкyжсЩЯШЁЕуGЃЌЪЙCGЃНCDЃН3ЃЌЙЙНЈЁїDCBЁеЁїGCBЃЌЧѓжБЯпBGЕФНтЮіЪНЃЌдйЧѓжБЯпBGгыХзЮяЯпНЛЕузјБъМДЮЊPЕуЃЌ
ЃЈ3ЃЉИљОнЦНааЫФБпаЮЕФЖдБпЦНааЧвЯрЕШЃЌРћгУЦНвЦЕФаджЪСаГіЗНГЬЧѓНтЃЌЗжЧщПіЬжТл.
НтЃКШчЭМЃК
ЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+4ЃЈaЁй0ЃЉгыxжсЃЌyжсЗжБ№НЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌЕуCШ§ЕуЃЎ
Ёр ![]() НтЕУ
НтЕУ![]()
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНЉx2+3x+4ЃЎ
ЃЈ2ЃЉДцдкЃЎРэгЩШчЯТЃК
yЃНЉx2+3x+4ЃНЉЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЎ
ЃЎ
ЁпЕуDЃЈ3ЃЌmЃЉдкЕквЛЯѓЯоЕФХзЮяЯпЩЯЃЌ
ЁрmЃН4ЃЌЁрDЃЈ3ЃЌ4ЃЉЃЌЁпCЃЈ0ЃЌ4ЃЉ
ЁпOCЃНOBЃЌЁрЁЯOBCЃНЁЯOCBЃН45ЁуЃЎ
СЌНгCDЃЌЁрCDЁЮxжсЃЌ
ЁрЁЯDCBЃНЁЯOBCЃН45ЁуЃЌ
ЁрЁЯDCBЃНЁЯOCBЃЌ
дкyжсЩЯШЁЕуGЃЌЪЙCGЃНCDЃН3ЃЌ
дйбгГЄBGНЛХзЮяЯпгкЕуPЃЌдкЁїDCBКЭЁїGCBжаЃЌCBЃНCBЃЌЁЯDCBЃНЁЯOCBЃЌCGЃНCDЃЌ
ЁрЁїDCBЁеЁїGCBЃЈSASЃЉ
ЁрЁЯDBCЃНЁЯGBCЃЎ
ЩшжБЯпBPНтЮіЪНЮЊyBPЃНkx+bЃЈkЁй0ЃЉЃЌАбGЃЈ0ЃЌ1ЃЉЃЌBЃЈ4ЃЌ0ЃЉДњШыЃЌЕУ
kЃНЉ![]() ЃЌbЃН1ЃЌ
ЃЌbЃН1ЃЌ
ЁрBPНтЮіЪНЮЊyBPЃНЉ![]() x+1ЃЎ
x+1ЃЎ
yBPЃНЉ![]() x+1ЃЌyЃНЉx2+3x+4
x+1ЃЌyЃНЉx2+3x+4
ЕБyЃНyBP ЪБЃЌЉ![]() x+1ЃНЉx2+3x+4ЃЌ
x+1ЃНЉx2+3x+4ЃЌ
НтЕУx1ЃНЉ![]() ЃЌx2ЃН4ЃЈЩсШЅЃЉЃЌ
ЃЌx2ЃН4ЃЈЩсШЅЃЉЃЌ
ЁрyЃН![]() ЃЌЁрPЃЈЉ
ЃЌЁрPЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉ![]()
![]()
![]() РэгЩШчЯТЃЌШчЭМ
РэгЩШчЯТЃЌШчЭМ
B(4ЃЌ0),C(0ЃЌ4) ЃЌХзЮяЯпЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ
ЩшN(![]() ЃЌn)ЃЌM(m, Љm2+3m+4)
ЃЌn)ЃЌM(m, Љm2+3m+4)
ЕквЛжжЧщПіЃКЕБMNгыBCЮЊЖдБпЙиЯЕЪБЃЌMNЁЮBC,MN=BC,
Ёр4-![]() =0-mЃЌЁрm=
=0-mЃЌЁрm=![]()
ЁрЉm2+3m+4=![]() ,
,
Ёр![]() ЃЛ
ЃЛ
ЛђЁр0-![]() =4-mЃЌ
=4-mЃЌ
Ёрm=![]()
ЁрЉm2+3m+4=![]() ,
,
Ёр![]() ЃЛ
ЃЛ
ЕкЖўжжЧщПіЃКЕБMNгыBCЮЊЖдНЧЯпЙиЯЕЃЌMNгыBCНЛЕуЮЊK,дђK(2,2)ЃЌ
Ёр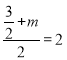
Ёрm=![]()
ЁрЉm2+3m+4=![]()
Ёр![]()
злЩЯЫљЪіЃЌЕБвдMЁЂNЁЂBЁЂCЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЕуMЕФзјБъЮЊ![]()
![]()
![]() .
.

 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ