题目内容
如图,等腰直角三角形ABC中,∠ACB=90°,AC=BC,M是△ABC内任意一点,连结MC并延长到E,使得CE=CM,以MA、MB为邻边做?MADB,对角线交点为F,连接DE.
(1)求证:①DE⊥AB;②DE=AB;
(2)若△ABC为等边三角形,猜想(1)中的两个结论是否成立?若成立,直接写出结论;若不成立,请直接写出你的猜想结果.
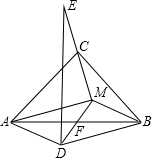
(1)求证:①DE⊥AB;②DE=AB;
(2)若△ABC为等边三角形,猜想(1)中的两个结论是否成立?若成立,直接写出结论;若不成立,请直接写出你的猜想结果.

证明:(1)连接CF,
∵四边形ADBM是平行四边形,
∴AF=BF,DF=MF,
又∵AC=BC,∠ACB=90°,
∴CF⊥AB,CF=
AB,
又∵MC=CE,
∴CF∥DE,CF=
DE,
∴DE⊥AB,DE=AB;
(2)①成立,②DE=
AB.
∵四边形ADBM是平行四边形,
∴AF=BF,DF=MF,
又∵△ABC为等边三角形,
∴AC=BC,∠ACB=∠ABC=60°,
∴CF⊥AB,CF=
AB,
又∵MC=CE,
∴CF∥DE,CF=
DE,
∴DE⊥AB,DE=
AB.

∵四边形ADBM是平行四边形,
∴AF=BF,DF=MF,
又∵AC=BC,∠ACB=90°,
∴CF⊥AB,CF=
| 1 |
| 2 |
又∵MC=CE,
∴CF∥DE,CF=
| 1 |
| 2 |
∴DE⊥AB,DE=AB;
(2)①成立,②DE=
| 3 |
∵四边形ADBM是平行四边形,
∴AF=BF,DF=MF,
又∵△ABC为等边三角形,
∴AC=BC,∠ACB=∠ABC=60°,
∴CF⊥AB,CF=
| ||
| 2 |
又∵MC=CE,
∴CF∥DE,CF=
| 1 |
| 2 |
∴DE⊥AB,DE=
| 3 |


练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目