题目内容
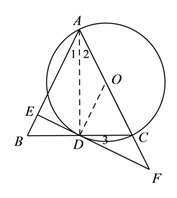
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.

【答案】(1)见解析;(2)6
【解析】试题分析:连接OD,则有OD⊥EF,然后证明OD//AB即可得;
(2)连接AD,则有∠ADB=90°,通过证明△FCD∽△FDA ,可得 FC:FD=CD:DA,再根据tan∠BDE=![]() ,通过推导即可得.
,通过推导即可得.
试题解析:(1)连接OD.∵EF切⊙O于点D,∴OD⊥EF.
又∵OD=OC,∴∠ODC=∠OCD,
∵AB=AC,∴∠ABC=∠OCD,∴∠ABC=∠ODC,
∴AB∥OD,∴DE⊥AB;
(2)连接AD.
∵AC为⊙O的直径,∴∠ADB=90°, ∴∠B+∠BDE=90°,∠B+∠1=90°,
∴∠BDE=∠1,
∵AB=AC,∴∠1=∠2,又∵∠BDE =∠3,∴∠2=∠3,
∴△FCD∽△FDA ,∴ ![]() ,
,
∵tan∠BDE=![]() ,∴tan∠2=
,∴tan∠2=![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵CF=3,∴FD=6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某学校对学生暑假参加志愿服务的时间进行抽样调查,将收集的数据分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组进行整理,并绘制成如下的统计图表(图中信息不完整).
五组进行整理,并绘制成如下的统计图表(图中信息不完整).

分组统计表
组别 | 志愿服务时间 | 人数 |
A |
|
|
B |
| 40 |
C |
|
|
D |
|
|
E |
| 16 |
请结合以上信息解答下列问题
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)补全“人数分组统计图①中![]() 组的人数和图②
组的人数和图②![]() 组和
组和![]() 组的比例值”;
组的比例值”;
(3)若全校学生人数为800人,请估计全校参加志愿服务时间在![]() 的范围的学生人数.
的范围的学生人数.



