题目内容
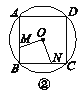
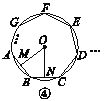
【题目】如图,在矩形![]() 中,点
中,点![]() 是
是![]() 的中点,
的中点,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在
恰好落在![]() 上
上![]() 点处,延长
点处,延长![]() ,
,![]() 交于点
交于点![]() .有下列四个结论:①
.有下列四个结论:①![]() 垂直平分
垂直平分![]() ;②
;②![]() 平分
平分![]() ;③
;③![]() ;④
;④![]() .其中,将正确结论的序号全部选对的是( )
.其中,将正确结论的序号全部选对的是( )
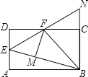
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
【答案】A
【解析】
由折叠的性质、矩形的性质与角平分线的性质,可证得CF=FM=DF;易求得∠BFE=∠BFN,则可得BF⊥EN;易证得△BEN是等腰三角形,但无法判定是等边三角形;故正确的结论有3个.
解:∵四边形ABCD是矩形,
∴∠D=∠BCD=90°,DF=MF,
由折叠的性质可得:∠EMF=∠D=90°,
即FM⊥BE,CF⊥BC,
∵BF平分∠EBC,
∴CF=MF,
∴DF=CF,在△DEF与△CFN中,
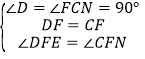
∴△DFE≌△CFN,
∴EF=FN,
∵∠BFM=90°∠EBF,∠BFC=90°∠CBF,
∴∠BFM=∠BFC,
∴BF平分∠MFC;故②正确;
∵∠MFE=∠DFE=∠CFN,
∴∠BFE=∠BFN,
∵∠BFE+∠BFN=180°,
∴∠BFE=90°,
即BF⊥EN,
∴BF垂直平分EN,故①正确;
∵∠BFE=∠D=∠FME=90°,
∴∠EFM+∠FEM=∠FEM+∠FBE=90°,
∴∠EFM=∠EBF,
∵∠DFE=∠EFM,
∴∠DFE=∠FBE,
∴△DEF∽△FEB;故③正确;
∵△DFE≌△CFN,∴BE=BN,
∴△EBN是等腰三角形,
∴∠N不一定等于60°,
故④错误.
故答案选:A.

练习册系列答案
相关题目