题目内容
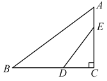
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,tanA=![]() .点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
.点D,E分别是边BC,AC上的点,且∠EDC=∠A.将△ABC沿DE所在直线对折,若点C恰好落在边AB上,则DE的长为___.
【答案】![]()
【解析】
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,根据折叠的性质得到DE⊥CF,OC=OF,再根据等角的余角相等得∠1=∠EDC,而∠EDC=∠A,则∠1=∠A,所以FC=FA,同理可得FC=FB,于是有CF=![]() AB,OC=
AB,OC=![]() AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=
AB,然后根据正切的定义和勾股定理得到BC=4,AB=5,所以OC=![]() ,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=
,再分别在Rt△OEC和Rt△ODC中,利用正切的定义计算出OE=![]() ,OD=
,OD=![]() ,再计算OE+OD即可.
,再计算OE+OD即可.
把△ABC沿DE对折,点C恰好落在AB的F点处,CF与DE相交于O点,如图,

∴DE⊥CF,OC=OF,
∵∠EDC+∠OCD=90°,∠1+∠OCD=90°,
∴∠1=∠EDC,
而∠EDC=∠A,
∴∠1=∠A,
∴FC=FA,
同理可得FC=FB,
∴CF=![]() AB,
AB,
∴OC=![]() AB,
AB,
在Rt△ABC中,∠C=90°,AC=3,
∴tanA=![]() ,
,
∴BC=4,
∴AB=![]() =5,
=5,
∴OC=![]() ,
,
在Rt△OEC中,tan∠1=tan∠A=![]() ,
,
∴OE=![]() ,
,
在Rt△ODC中,tan∠ODC=tan∠A=![]() ,
,
∴OD=![]() ,
,
∴DE=OD+OE=![]() +
+![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目





