Question

【题目】如图，在△ABC中，D是AC上一点，联结BD，∠CBD=∠A．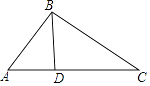
（1）求证：△CBD∽△CAB；
（2）若D是AC中点，CD=3，求BC的长．

Answer 1

【答案】
（1）证明：∵∠CBD=∠A，∠C是公共角，

∴△CBD∽△CAB

（2）解：∵D是AC中点，CD=3，

∴AC=2AD=6．

∵△CBD∽△CAB，

∴ = ，即BC2=ACCD=6×3=18，

∴BC=3

【解析】（1）根据∠CBD=∠A，∠C是公共角即可得出结论；（2）根据（1）中△CBD∽△CAB即可得出结论．
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识，掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．