题目内容
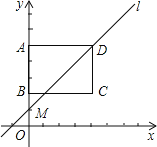
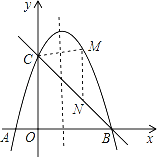
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,已知A(﹣1,0),C(0,3)
(1)求该抛物线的表达式;
(2)求BC的解析式;
(3)点M是对称轴右侧点B左侧的抛物线上一个动点,当点M运动到什么位置时,△BCM的面积最大?求△BCM面积的最大值及此时点M的坐标.

【答案】(1)抛物线的解析式y=-x2+2x+3;(2)BC的解析式为y=-x+3;(3)△BCM面积的最大值为![]() ,此时点M的坐标(
,此时点M的坐标(![]() ,
, ![]() ).
).
【解析】试题分析:
(1)将A、C坐标代入y=﹣x2+bx+c列方程组求得b、c的值即可求得解析式;
(2)由(1)中所求解析式可求得B的坐标,结合点C的坐标,用待定系数法可求得直线BC的解析式;
(3)过点M作MN∥y轴,交BC于点N,设点M的横坐标为“m”,则由(1)、(2)所得解析式可表达出M、N的纵坐标,从而可表达出MN的长度,在由S△BCM=![]() MN·OB即可用含“m”的式子表达出“S△BCM”,即可求得其最大值和此时点M的坐标.
MN·OB即可用含“m”的式子表达出“S△BCM”,即可求得其最大值和此时点M的坐标.
试题解析:
(1)将A、C点坐标代入函数解析式,得![]() ,
,
解得![]()
抛物线的解析式y=-x2+2x+3;
(2)当y=0时,有-x2+2x+3=0,解得:x1=-1,x2=3,
∴点B的坐标为:(3,0),
设直线BC的解析式为:y=kx+n,把B、C的坐标代入可得: ![]() 解得;
解得; ![]() ,∴直线BC的解析式为:y=-x+3;
,∴直线BC的解析式为:y=-x+3;
(3)如图,过点M作MN∥y轴,交BC于点N,
设点M的坐标为![]() ,则点N的坐标为
,则点N的坐标为![]() ,
,
又∵点M在点N的上方,
∴MN=![]() ,
,
∴S△BCM=![]() MN·OB
MN·OB
=![]()
= ![]()
=![]() .
.
∵点M是对称轴右侧、点B左侧的抛物线上一个动点,
∴![]() ,
,
∴当![]() 时,S△BCM最大=
时,S△BCM最大=![]() .此时点M的坐标为
.此时点M的坐标为![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目