Question

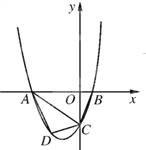
【题目】如图，在RtABC 中， BAC 90， AB AC ，点 D 是 AB 的中点，AF CD 于 H 交 BC 于 F， BE AC 交 AF 的延长线于 E.

求证：（1）ADC ≌ BEA

（2）BC 垂直平分 DE.

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）根据ASA即可证明△DBP≌△EBP；

（2）想办法证明△DBP≌△EBP（SAS）即可解决问题.

证明：（1）由题意可知，∠DAH+∠ADH=90°，∠ACH+∠ADH=90°，

∴∠DAH=∠ACH，

∵∠BAC=90°，BE∥AC，

∴∠CAD=∠ABE=90°．

又∵AB=CA，

∴在△ABE与△CAD中，

，

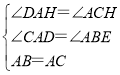∴△ABE≌△CAD（ASA）．

（2）∵△ABE≌△CAD，

∴AD=BE，

又∵AD=BD，

∴BD=BE，

在Rt△ABC中，∠ACB=45°，∠BAC=90°，AB=AC，

故∠ABC=45°．

∵∠ABE=90°，

∴∠EBF=90°-45°=45°，

∴△DBP≌△EBP（SAS），

∴DP=EP，

即可得出BC垂直且平分DE．