��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��B��C������ֱ�Ϊ��0��5������0��2������4��2����ֱ��l�Ľ���ʽΪy=kx+5-4k��k��0����
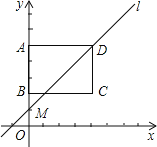
��1����ֱ��l������Bʱ����һ�κ����Ľ���ʽ��
��2��ͨ������˵��������kΪ��ֵ��ֱ��l�ܾ�����D��
��3��ֱ��l��y�ύ�ڵ�M����N���߶�DM�ϵ�һ�㣬����NBDΪ���������Σ���̽����������y=kx+5-4kΪ����������ʱ����N�ĸ�����______����
���𰸡���1��y=![]() x+2����2�������������3��2.
x+2����2�������������3��2.
��������
��1������B����������ʽ����⣻
��2��������ɵõ�D��4��5������y=kx+5-4k=k��x-4��+5��֪����x-4=0ʱ������kΪ��ֵ��ֱ��l�ܾ����㣨4��5�������ɵý��ۣ�
��3�����������k=![]() ���������O���M�غϣ����������ε����ʿ����N�ĸ�����
���������O���M�غϣ����������ε����ʿ����N�ĸ�����
�⣺��1����ֱ��l������B��0��2����
��2=5-4k
��k=![]()
��һ�κ�������ʽΪ��y=![]() x+2
x+2
��2����A��B��C������ֱ�Ϊ��0��5������0��2������4��2����
���D��4��5��
��y=kx+5-4k=k��x-4��+5
�൱x=4ʱ��y=5��
���kΪ��ֵ��ֱ��l�ܾ����㣨4��5��
������kΪ��ֵ��ֱ��l�ܾ�����D��
��3���ߺ���y=kx+5-4kΪ����������
��5-4k=0
��k=![]()
�ຯ������ʽΪ��y=![]() x
x
���M���O�غϣ���ͼ����BM=2
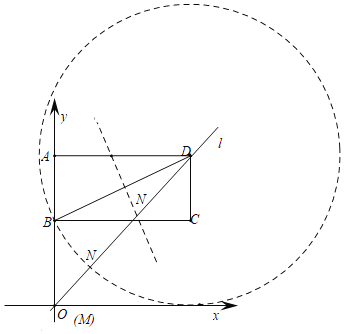
�ߡ�NBDΪ���������Σ�
����BD�Ĵ�ֱƽ���߽�DO�ڵ�N�����Ե�DΪԲ�ģ�BDΪ�뾶��Բ�����߶�DO�ڵ�N
���N�ĸ���Ϊ2��
�ʴ�Ϊ��2

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�