ЬтФПФкШн
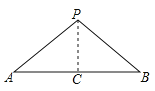
ЁОЬтФПЁП(1)ШчЭМ 1ЃЌШє PЪЧПкABCD Бп CD ЩЯШЮвтвЛЕуЃЌСЌНс APЁЂBPЃЌШєЁїAPB ЕФУцЛ§ЮЊ 60 ЃЌЁїAPD ЕФУцЛ§ЮЊ 18ЃЌдђ SЁїAPC= .
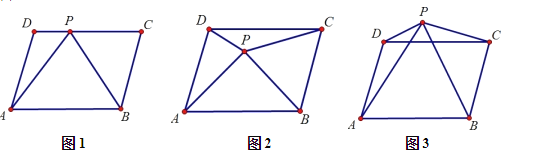
(2) ШчЭМ 2ЃЌЂйШєЕу P дЫЖЏЕНПкABCD ФквЛЕуЪБЃЌЪдЫЕУї SЁїAPB +SЁїDPC =SЁїBPC +SЁїAPD.
ЂкШєДЫЪБЁїAPB ЕФУцЛ§ЮЊ 60ЃЌЁїAPD ЕФУцЛ§ЮЊ 18ЃЌдђ SЁїAPC= .
ЃЈ3ЃЉШчЭМ 3ЂйРћгУЃЈ2ЃЉжаЕФЗНЗЈФуЛсЗЂЯжЃЌSЁїAPB ЃЌSЁїDPC ЃЌSЁїBPC ЃЌSЁїAPD жЎМфДцдкдѕбљЕФЙиЯЕЃК .
ЂкШєДЫЪБЁїAPB ЕФУцЛ§ЮЊ 60ЃЌЁїAPD ЕФУцЛ§ЮЊ 18ЃЌЧыРћгУФуЕФЗЂЯжЃЌЧѓ SЁїAPC ЕФУцЛ§ЃП
ЁОД№АИЁПЃЈ1ЃЉ42ЃЛЃЈ2ЃЉЂйРћгУЭЌЕзЕШИпЃЌЂк42ЃЛЃЈ3ЃЉЂйSЁїAPB - SЁїDPC =SЁїBPC +SЁїAPD
Ђк42.
ЁОНтЮіЁП
ЃЈ1ЃЉзї![]() НЛABгкЕуEЃЌИљОн
НЛABгкЕуEЃЌИљОн
![]() МДПЩЧѓНт.
МДПЩЧѓНт.
(2) ЂйЙ§ЕуPзїPEЁЭABгкЕуEЃЌбгГЄEPНЛDCгкЕуFЃЌгЩШ§НЧаЮЕФУцЛ§ЙЋЪНПЩЕУ![]() SЫФБпаЮABCDЃЌНјЖјПЩЕУSЁїPAD+SЁїPBC=
SЫФБпаЮABCDЃЌНјЖјПЩЕУSЁїPAD+SЁїPBC=![]() SЫФБпаЮABCDЮЪЬтЕУНтЃЎ
SЫФБпаЮABCDЮЪЬтЕУНтЃЎ
ЂкИљОн(2)ЂйжаЕФНсТлМДПЩЧѓНт.
ЃЈ3ЃЉЂйВЮее(2) ЂйзїГіИЈжњЯпЃЌИљОнУцЛ§ЙЋЪНМДПЩЧѓНт.
ЂкИљОн(2)ЂкжаЕФНтЬтВНжшМДПЩЧѓНт.
ЃЈ1ЃЉзї![]() НЛABгкЕуEЃЌ
НЛABгкЕуEЃЌ
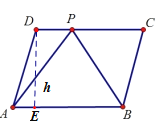
![]()
![]()
![]()
ЃЈ2ЃЉЂйЙ§ЕуPзїPEЁЭABгкЕуEЃЌбгГЄEPНЛDCгкЕуFЃЌ
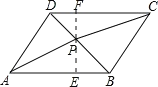
![]() SЫФБпаЮABCDЃЌ
SЫФБпаЮABCDЃЌ
ЭЌРэПЩЕУЃКSЁїPAD+SЁїPBC=![]() SЫФБпаЮABCDЁЃ
SЫФБпаЮABCDЁЃ
![]()
ЂкЁп![]()
Ёр![]()
МД![]()
ЙЪД№АИЮЊЃК42.
ЃЈ3ЃЉЂйЙ§ЕуPзїPMЁЭCDгкЕуNЃЌбгГЄPNНЛABгкЕуMЃЌ
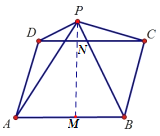
![]() SЫФБпаЮABCDЃЌ
SЫФБпаЮABCDЃЌ
ЭЌРэПЩЕУЃКSЁїPAD+SЁїPBC=![]() SЫФБпаЮABCDЁЃ
SЫФБпаЮABCDЁЃ
![]()
ЂкЁп![]()
Ёр![]()
МД![]()
ЙЪД№АИЮЊЃК42.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИЁОЬтФПЁПФГЪаЖдМДНЋВЮМгжаПМЕФ4000УћГѕжаБЯвЕЩњНјааСЫвЛДЮЪгСІГщбљЕїВщЃЌЛцжЦГіЦЕЪ§ЗжВМБэКЭВЛЭъећЕФЦЕЪ§ЗжВМжБЗНЭМЃЎЧыИљОнЭМБэаХЯЂЛиД№ЯТСаЮЪЬтЃК
ГѕжаБЯвЕЩњЪгСІГщбљЕїВщЦЕЪ§ЗжВМБэ
ЪгСІ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
4.0ЁмxЃМ4.3 | 20 | 0.1 |
4.3ЁмxЃМ4.6 | 40 | 0.2 |
4.6ЁмxЃМ4.9 | 70 | 0.35 |
4.9ЁмxЃМ5.2 | a | 0.3 |
5.2ЁмxЃМ5.5 | 10 | b |

ЃЈ1ЃЉБОДЮЕїВщбљБОШнСПЮЊЁЁ ЁЁЃЛ
ЃЈ2ЃЉдкЦЕЪ§ЗжВМБэжаЃЌaЃН ЁЁЃЌbЃНЁЁ ЁЁЃЌВЂНЋЦЕЪ§ЗжВМжБЗНЭМВЙГфЭъећЃЛ
ЃЈ3ЃЉШєЪгСІдк4.9вдЩЯЃЈКЌ4.9ЃЉОљЪєБъзМЪгСІЃЌИљОнЩЯЪіаХЯЂЙРМЦШЋЧјГѕжаБЯвЕЩњжаДяЕНБъзМЪгСІЕФбЇЩњдМгаЖрЩйШЫЃП