题目内容
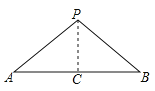
【题目】如图,等腰△ABC中,CA=CB=4,∠ACB=120°,点D在线段AB上运动(不与A、B重合),将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ.
(1)证明:CP=CQ;
(2)求∠PCQ的度数;
(3)当点D是AB中点时,请直接写出△PDQ是何种三角形.
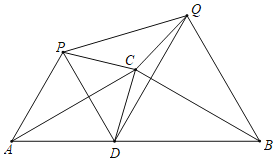
【答案】(1)见解析;(2)∠PCQ=120°;(3)△PDQ是等边三角形.
【解析】
(1)由折叠直接得到结论;
(2)由折叠的性质求出∠ACP+∠BCQ=120°,再用周角的意义求出∠PCQ=120°;
(3)先判断出△APD是等边三角形,△BDQ是等边三角形,再求出∠PDQ=60°,即可.
(1)∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴CP=CD=CQ;
(2)∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴∠ACP=∠ACD,∠BCQ=∠BCD,
∴∠ACP+∠BCQ=∠ACD+∠BCD=∠ACB=120°,
∴∠PCQ=360°-(∠ACP+BCQ+∠ACB)=360°-(120°+120°)=120°;
(3)△PDQ是等边三角形.
理由:∵将△CAD与△CBD分别沿直线CA、CB翻折得到△CAP与△CBQ,
∴AD=AP,∠DAC=∠PAC,
∵∠DAC=30°,
∴∠PAD=60°,
∴△APD是等边三角形,
∴PD=AD,∠ADP=60°,
同理:△BDQ是等边三角形,
∴DQ=BD,∠BDQ=60°,
∴∠PDQ=60°,
∵当点D在AB的中点,
∴AD=BD,
∴PD=DQ,
∴△DPQ是等边三角形

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】某市对即将参加中考的4000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和不完整的频数分布直方图.请根据图表信息回答下列问题:
初中毕业生视力抽样调查频数分布表
视力 | 频数(人) | 频率 |
4.0≤x<4.3 | 20 | 0.1 |
4.3≤x<4.6 | 40 | 0.2 |
4.6≤x<4.9 | 70 | 0.35 |
4.9≤x<5.2 | a | 0.3 |
5.2≤x<5.5 | 10 | b |

(1)本次调查样本容量为 ;
(2)在频数分布表中,a= ,b= ,并将频数分布直方图补充完整;
(3)若视力在4.9以上(含4.9)均属标准视力,根据上述信息估计全区初中毕业生中达到标准视力的学生约有多少人?