题目内容
【题目】（1）将直角三角形ABC（∠C为直角）按如图1放置，使得坐标原点与点C重合，已知A（a,3）,B(b,-3),且a+b=8,求三角形ACB的面积：
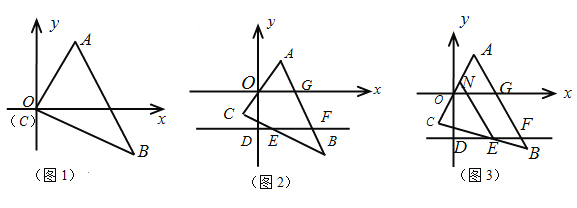
（2）将直角三角形ACB（∠C为直角）按如图2方式放置，使得点O在边AC上，D是y轴上一点，过D作DF//x轴，交AB于F点，AB交x轴于点G, BC交DF于点E, 若∠AOG=50°，求∠BEF的度数。
将直角三角形ACB（∠C为直角）按照如图3方式放置，使得∠C在x轴于DF之间，N为AC边上一点，且∠NEC+∠CEF=180°，写出∠NEF与∠AOG之间的数量关系，并证明你的结论。
【答案】（1）12（2）40°（3）∠NEF=2∠AOG
【解析】（1）作AM⊥y轴与M,作BN⊥y轴于N，
∴
=
=
过C作CM//x轴，∴∠ACM =∠AOG=50°，
而∠BEF=∠CED=∠MCE
∴∠BEF=∠ACB-∠ACM =40°
(3)过C作CM//x轴，设∠NEC=x，∠NEF=y，∠AOG= z
∵∠NEC+∠CEF=180°, 而∠NEC+∠NEF+∠BEF=180°，
∴∠NEC=∠BEF= x
∴∠NEF+2∠NEC=180°,即2 x+ y=180°, ①
∵∠BEF=∠CED=∠MCE= x，∠AOG=∠ACM= z
∴∠ACB=∠ACM+∠MCE= 90°, 即x+z=90°, ②
①-②×2, 得：y=2 z
∴∠NEF=2∠AOG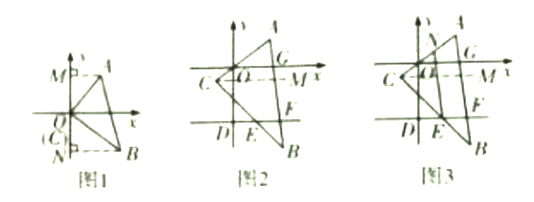 
练习册系列答案
相关题目
