题目内容
【题目】(8分)如图,在Rt△ABC中,∠ACB=Rt∠。
(1)请用直尺和圆规,过点C作AB边上的高线,交AB于D,作∠B的角平分线,交AC于E,交CD与F。
(2)△CEF是什么三角形,请说明理由
【答案】 (1) 图略;(2)等腰三角形,理由略
【解析】试题分析:(1)直接利用垂线的作法以及角平分线的作法得出D,E,F,点的位置;(2)根再由据对顶角的性质和和直角三角形两锐角互余的性质可得∠CFE=∠DFB=90°﹣∠FBD,
∠CEB=∠A+∠FBA=90°﹣∠CBE=90°﹣∠EBA=∠BFD,即可得∠CEF=∠CFE,由此即可得结论.
试题解析:
(1)如图所示:点D,E,F即为所求;
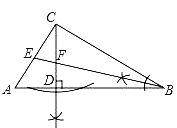
(2)△CEF是等腰三角形,
理由:∵∠CFE=∠DFB=90°﹣∠FBD,
∠CEB=∠A+∠FBA=90°﹣∠CBE=90°﹣∠EBA=∠BFD,
∴∠CEF=∠CFE,
∴△CEF是等腰三角形.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目