题目内容
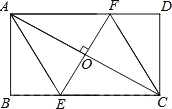
【题目】(2016广西省贺州市第23题)如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
【答案】(1)、证明过程见解析;(2)、2![]()
【解析】
试题分析:(1)、由过AC的中点O作EF⊥AC,根据线段垂直平分线的性质,可得AF=CF,AE=CE,OA=OC,然后由四边形ABCD是矩形,易证得△AOF≌△COE,则可得AF=CE,继而证得结论;(2)、由四边形ABCD是矩形,易求得CD的长,然后利用三角函数求得CF的长,继而求得答案.
试题解析:(1)、∵O是AC的中点,且EF⊥AC, ∴AF=CF,AE=CE,OA=OC,
∵四边形ABCD是矩形, ∴AD∥BC, ∴∠AFO=∠CEO, ∴△AOF≌△COE(AAS), ∴AF=CE,
∴AF=CF=CE=AE, ∴四边形AECF是菱形;
(2)、∵四边形ABCD是矩形, ∴CD=AB=![]() , 在Rt△CDF中,cos∠DCF=
, 在Rt△CDF中,cos∠DCF=![]() ,∠DCF=30°,
,∠DCF=30°,
∴CF=![]() =2, ∵四边形AECF是菱形, ∴CE=CF=2, ∴四边形AECF是的面积为:ECAB=2
=2, ∵四边形AECF是菱形, ∴CE=CF=2, ∴四边形AECF是的面积为:ECAB=2![]() .
.

练习册系列答案
相关题目
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?